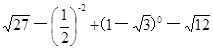小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如：3＋2＝(1＋)2，善于思考的小明进行了以下探索：
设a＋b＝(m＋n)2（其中a、b、m、n均为整数），
则有a＋b＝m2＋2n2＋2mn．
∴a＝m2＋2n2，b＝2mn．这样小明就找到了一种把部分a＋b的式子化为平方 式的方法．
请仿照小明的方法探索并解决下列问题：
（1）当a、b、m、n均为正整数时，若a＋b＝(m＋n)2，用含m、n的式子分别表示a、b，得a＝_ ，b＝_ ；
（2）利用所探索的结论，找一组正整数a、b、m、n，
填空：_ ＋_ ＝(_ ＋_ )2；
（3）若a＋4＝(m＋n)2，且a、m、n均为正整数，求a的值．
甲、乙两辆汽车分别从A、B两地同时出发，沿同一条公路相向而行．乙车出发2h休息．与甲车相遇．继续行驶．设甲、乙两车与B地的距离y（km）与行驶的时间x（h）之间的函数图象如图所示．
（1）写出甲车与B地的距离y（km）与行驶时间x（h）之间的函数关系式 ；
（2）乙车休息的时间为 ；
（3）写出休息前，乙车与B地的距离y（km）与行驶的时间x（h）之间的函数关系式 ；休息后，乙车与B地的距离y（km）与行驶的时间x（h）之间的函数关系式 ；
（4）求行驶多长时间两车相距100km．
根据图中给出的信息，解答下列问题：
（1）放入一个小球水面升高 cm，放入一个大球水面升高 cm；
（2）如果要使水面上升到50cm，应放入大球、小球各多少个？
如图，已知：DE⊥AO于点E，BO⊥AO于点O，∠CFB=∠EDO，证明：CF∥DO.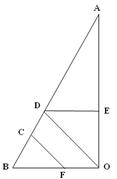
已知：正比例函数y=（m﹣1）
的图象在第二、四象限，求m的值．
计算：