已知: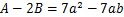 ,且
,且 .
.
(1)求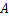 等于多少?
等于多少?
(2)若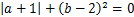 ,求
,求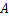 的值.
的值.
已知:一次函数y=2x+1与y轴交于点C,点A(1,n)是该函数与反比例函数 在第一象限内的交点.
在第一象限内的交点.
(1)求点 的坐标及
的坐标及 的值;
的值;
(2)试在 轴上确定一点
轴上确定一点 ,使
,使 ,求出点
,求出点 的坐标.
的坐标.
如图,在△ABC中,BD⊥AC于点D, ,
, ,并且
,并且 .求
.求 的长.
的长.
已知:二次函数 的图象开口向上,并且经过原点
的图象开口向上,并且经过原点
 .
.
(1)求 的值;
的值;
(2)用配方法求出这个二次函数图象的顶点坐标.
已知:抛物线 与x轴交于点A、B(A左B右),其中点B的坐标为(7,0),设抛物线的顶点为C.
与x轴交于点A、B(A左B右),其中点B的坐标为(7,0),设抛物线的顶点为C.
(1)求抛物线的解析式和点C的坐标;
(2)如图1,若AC交y轴于点D,过D点作DE∥AB交BC于E.点P为DE上一动点,PF⊥AC于F,PG⊥BC于G.设点P的横坐标为a,四边形CFPG的面积为y,求y与a的函数关系式和y的最大值;
(3)如图2,在条件(2)下,过P作PH⊥x轴于点H,连结FH、GH,是否存在点P,使得△PFH与△PHG相似?若存在,求出P点坐标;若不存在,说明理由.
观察计算:
当 ,
, 时,
时, 与
与 的大小关系是_________________.
的大小关系是_________________.
当 ,
, 时,
时, 与
与 的大小关系是_________________.
的大小关系是_________________.
探究证明:
如图所示, 为圆O的内接三角形,
为圆O的内接三角形, 为直径,过C作
为直径,过C作 于D,设
于D,设 ,BD=b.
,BD=b.
(1)分别用 表示线段OC,CD;
表示线段OC,CD;
(2)探求OC与CD表达式之间存在的关系(用含a,b的式子表示).
归纳结论:
根据上面的观察计算、探究证明,你能得出 与
与 的大小关系是:______________.
的大小关系是:______________.
实践应用:
要制作面积为4平方米的长方形镜框,直接利用探究得出的结论,求出镜框周长的最小值.