对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(m/s)的数据如下表.
| 甲 |
27 |
38 |
30 |
37 |
35 |
31 |
| 乙 |
33 |
29 |
38 |
34 |
28 |
36 |
(1)画出茎叶图,由茎叶图你能获得哪些信息?
(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、中位数、方差,并判断选谁参加比赛更合适.
已知函数 .
.
(1)当 时,求
时,求 的单调区间;
的单调区间;
(2)若不等式 有解,求实数m的取值菹围;
有解,求实数m的取值菹围;
(3)证明:当a=0时, .
.
如图,在三棱锥 中,直线
中,直线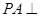 平面
平面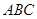 ,且
,且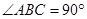 ,又点
,又点 ,
, ,
,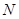 分别是线段
分别是线段 ,
,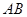 ,
, 的中点,且点
的中点,且点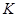 是线段
是线段 上的动点.
上的动点.
证明:直线 平面
平面 ;
;
(2) 若 ,求二面角
,求二面角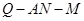 的平面角的余弦值.
的平面角的余弦值.
设数列 的前
的前 项和为
项和为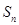 ,
,
已知 ,
, ,
, ,
,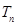 是数列
是数列 的前
的前 项和.
项和.
(1)求数列 的通项公式;(2)求
的通项公式;(2)求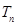 ;
;
(3)求满足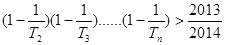 的最大正整数
的最大正整数 的值.
的值.
已知角A、B、C为△ABC的三个内角,其对边分别为a、b、c,若 =(-cos
=(-cos ,sin
,sin ),
), =(cos
=(cos ,sin
,sin ),a=2
),a=2 ,且
,且 ·
· =
= .
.
(1)若△ABC的面积S= ,求b+c的值.
,求b+c的值.
(2)求b+c的取值范围.
已知 (
( )
)
(1)若方程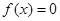 有3个不同的根,求实数
有3个不同的根,求实数 的取值范围;
的取值范围;
(2)在(1)的条件下,是否存在实数 ,使得
,使得 在
在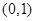 上恰有两个极值点
上恰有两个极值点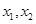 ,且满足
,且满足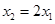 ,若存在,求实数
,若存在,求实数 的值,若不存在,说明理由.
的值,若不存在,说明理由.