如图△ABC中，∠C=90º，∠A=30º，BC=5cm；△DEF中，∠D=90º,∠E=45º,DE=3cm.现将△DEF的直角边DF与△ABC的斜边AB重合在一起，并将△DEF沿AB方向移动（如图）.在移动过程中，D、F两点始终在AB边上（移动开始时点D与点A重合，一直移动至点F与点B重合为止）.
（1）在△DEF沿AB方向移动的过程中，有人发现：E、B两点间的距离随AD的变化而变化，现设AD="x,BE=y," 请你写出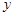
与
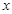之间的函数关系式及其定义域.
（2）请你进一步研究如下问题：
问题①：当△DEF移动至什么位置，即AD的长为多少时，E、B的连线与AC平行？
问题②：在△DEF的移动过程中，是否存在某个位置，使得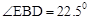
？如果存在，求出AD的长度；如果不存在，请说明理由.
问题③：当△DEF移动至什么位置，即AD的长为多少时，以线段AD、EB、BC的长度为三边长的三角形是直角三角形？
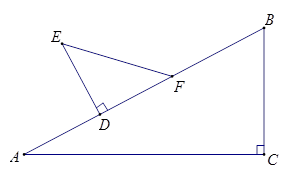
如图，点B是△ADC的边AD的延长线上一点，若∠C=50°，∠BDE=60°，∠ADC=70°．求证：DE∥AC．
解方程组：
．
如图，点C在∠MAN的边AM上，CD⊥AN，垂足为点D，点B在边AN上运动，∠BCA的平分线交AN于点E。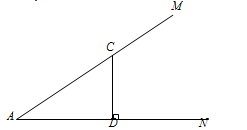
（1）若∠A＝30°，∠B＝70°，求∠ECD的度数；
（2）若∠A＝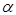
，∠B＝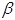
，求∠ECD的度数（用含
的式子表示）．
某校准备组织七年级400名学生参加北京夏令营，已知用3辆小客车和1辆大客车每次可运送学生105人；用1辆小客车和2辆大客车每次可运送学生110人；
（1）每辆小客车和每辆大客车各能坐多少名学生？
（2）若学校计划租用小客车x辆，大客车y辆，一次送完，且恰好每辆车都坐满；
①请你设计出所有的租车方案；
②若小客车每辆需租金4000元，大客车每辆需租金7600元，请选出最省钱的租车方案，并求出最少租金．
已知x＋y＝3，且（x＋2）（y＋2）＝12．
（1）求xy的值；（2）求x2＋3xy＋y2的值．