如图所示，aa′、bb′、cc′、dd′为区域Ⅰ、Ⅱ、Ⅲ的竖直边界，三个区域的宽度相同，长度足够大，区域Ⅰ、Ⅲ内分别存在垂直纸面向外和向里的匀强磁场，区域Ⅱ存在竖直向下的匀强电场．一群速率不同的带正电的某种粒子，从边界aa′上的O处，沿着与Oa成30°角的方向射入Ⅰ区．速率小于某一值的粒子在Ⅰ区内运动时间均为t0；速率为v0的粒子在Ⅰ区运动
后进入Ⅱ区．已知Ⅰ区的磁感应强度的大小为B，Ⅱ区的电场强度大小为2Bv0，不计粒子重力．求：
(1)该种粒子的比荷
；
(2)区域Ⅰ的宽度d；
(3)速率为v0的粒子在Ⅱ区内运动的初、末位置间的电势差U；
(4)要使速率为v0的粒子进入Ⅲ区后能返回到Ⅰ区，Ⅲ区的磁感应强度B′的大小范围应为多少？
在研究摩擦力特点的实验中，将木块放在足够长的静止水平木板上．如图11甲所示，用力沿水平方向拉木块，使拉力F从0开始逐渐增大．经实验绘制出摩擦力Ff随拉力F的变化图象如图丙所示．已知木块质量为0.78 kg.
求木块与长木板间的动摩擦因数．
若木块在与水平方向成θ＝37°角斜向右上方的恒定拉力F′作用下，以a＝2.0 m/s2的加速度从静止开始做匀加速直线运动，如图乙所示．则F′为多大？
(取sin 37°＝0.6，cos 37°＝0.8)
如图，用一根绳子a把物体挂起来，再用另一根水平的绳子b 把物体拉向一旁固定起来。物体的重力是40 N，绳子a与竖直方向的夹角q = 37°，绳子a与b对物体的拉力分别是多大？
(sin 37° = 0.6，cos 37° = 0.8)
如图所示，质量M =" 10" kg的木楔ABC静置于粗糙水平地面上，动摩擦因数= 0.02， 在木楔的倾角为30°的斜面上，有一质量m =" 1.0" kg的物块由静止开始沿斜面下滑，当滑行路程x =" 1.4" m时，其速度v =" 1.4" m/s，在这过程中木楔没有动。求地面对木楔的摩擦力的大小和方向。 
为了安全，在公路上行驶的汽车之间应保持必要的距离。已知某公路的最高限速 v =" 72" km/h。假设前方车辆突然停止，后车司机从发现这一情况，经操纵刹车，到汽车开始减速所经历的时间(即反应时间)t =" 0.50" s。刹车时汽车的加速度大小为4 m/s2。该高速公路上汽车间的距离至少应为多少？
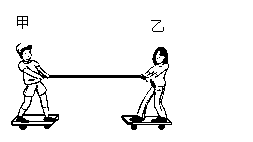
如图所示，男生甲和女生乙各站在一块滑板上，分别抓着轻绳的一端。甲与滑板的总质量为60 kg，乙与滑板的总质量为50 kg。忽略地面摩擦力。当甲以30 N的力量收回绳子时，乙双手不动，只紧抓着绳子。在收绳过程中，是不是只有一人移动？
求两人各自的加速度的大小和方向。
