如图所示,有一长为L的细线,细线的一端固定在O点,另一端拴一质量为m的小球,现使小球恰好在竖直平面内做完整的圆周运动,已知水平面上的C点在O点的正下方,且到O点的距离为1.9 L,不计空气阻力,求:(g=10 m/s2)
(1)小球通过最高点A的速度vA;
(2)若小球通过最低点B时,细线对小球的拉力T恰好为小球重力的6倍,且小球通过B点时细线断裂,求小球落地点到C的距离.
如图所示,在足够长的绝缘板MN上方距离为d的O点处,水平向左发射一个速率为v0,质量为 、电荷为
、电荷为 的带正电的粒子(不考虑粒子重力)。
的带正电的粒子(不考虑粒子重力)。
(1)若在绝缘板上方加一电场强度大小为 、方向竖直向下的匀强电场,求带电粒子打到板上距P点的水平距离(已知
、方向竖直向下的匀强电场,求带电粒子打到板上距P点的水平距离(已知 );
);
(2)若在绝缘板的上方只加一方向垂直纸面,磁感应强度 的匀强磁场,求:①带电粒子在磁场中运动半径; ②若O点为粒子发射源,能够在纸面内向各个方向发射带电粒子(不考虑粒子间的相互作用),求发射出的粒子打到板上的最短时间。
的匀强磁场,求:①带电粒子在磁场中运动半径; ②若O点为粒子发射源,能够在纸面内向各个方向发射带电粒子(不考虑粒子间的相互作用),求发射出的粒子打到板上的最短时间。
如图所示为质谱仪上的原理图,M为粒子加速器,电压为U1=5000V;N为速度选择器, 磁场与电场正交,磁感应强度为B1=0.2T,板间距离为d =0.06m;P为一个边长为l的正方形abcd的磁场区,磁感应强度为B2=0.1T,方向垂直纸面向外,其中dc的中点S开有小孔,外侧紧贴dc放置一块荧光屏。今有一比荷为 的正离子从静止开始经加速后,恰好通过速度选择器,从a孔以平行于ab方向进入abcd磁场区,正离子刚好经过小孔S 打在荧光屏上。求:
的正离子从静止开始经加速后,恰好通过速度选择器,从a孔以平行于ab方向进入abcd磁场区,正离子刚好经过小孔S 打在荧光屏上。求: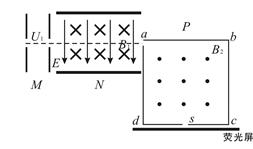
(1)粒子离开加速器时的速度v;
(2)速度选择器的电压U2;
(3)正方形abcd边长l。
如图所示,用电阻为R的硬导线做成一边长为L的方框。将方框放在绝缘的水平木板上,与木板最大的摩擦力为 。在方框右半部加上均匀增加的竖直向下的磁场区域中,磁感应强度
。在方框右半部加上均匀增加的竖直向下的磁场区域中,磁感应强度 。求:
。求:
(1)导线中感应电流的大小;
(2)经过多少时间方框开始运动。
如图所示,在竖直平面内有两个等量的异种点电荷,其电荷量分别为+Q、-Q,固定在同一个水平直线上相距为 的A、B两点。在AB连线的垂直平分线有固定光滑竖直绝缘杆,在C点有一个质量为m、电荷量为-q小环(可视为点电荷)静止释放。已知ABC构成正三角形,求:
的A、B两点。在AB连线的垂直平分线有固定光滑竖直绝缘杆,在C点有一个质量为m、电荷量为-q小环(可视为点电荷)静止释放。已知ABC构成正三角形,求:
(1)在C点杆对小环的作用力大小;
(2)小环滑到D点的速度大小。
如图所示,质量分别为M和m的两个小物块用轻绳连接,绳跨过倾角α=37°的斜面顶端的定滑轮,绳平行于斜面,滑轮与转轴之间的摩擦不计,已知M=2m=2kg。开始时,用手托物块M,使M离水平面的高度为h=0.5m,物块m静止在斜面底端。撤去手,使M和m从静止开始做匀加速直线运动,经过t=0.5s,M落到水平面上,停止运动,由于绳子松弛,之后物块m不再受到绳子的拉力作用。求:(g取10m/s2)
(1)物块M竖直向下运动过程加速度的大小;
(2)物块m所受到的摩擦力大小
(3)物块m沿斜面运动的最大距离?(假设斜面足够长)