(1)我国科学家经过艰苦努力，率先建成了世界上第一个全超导托克马克试验装置并调试成功．这种装置被称为“人造太阳”，它能够承受上亿摄氏度高温且能够控制等离子态的核子发生聚变并稳定持续地输出能量，就像太阳一样为人类提供无限清洁能源．在该装置内发生的核反应方程是
H＋
H―→
He＋X，其中粒子X的符号是________．已知H的质量是m1， H的质量是m2，He的质量是m3，X的质量是m4，光速是c，则发生一次上述聚变反应所释放的核能表达式为___________________________________________．
(2)光滑水平面上静止放置一长方形木板B，B的质量为M＝2 kg，B的右端离竖直墙6 m．现有一小物体A，其质量m＝1 kg，以v0＝6 m/s的速度从B的左端水平滑上B，如图所示．A和B之间的动摩擦因数μ＝0.4，B与墙碰撞时间极短，且碰撞时无能量损失．要使A最终不脱离B，B的最短长度是多少？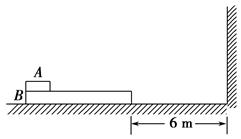
如图所示，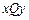
是位于足够大的绝缘光滑水平桌面内的平面直角坐标系，虚线MN是∠
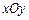的角平分线．在MN的左侧区域，存在着沿
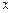轴负方向、场强为E的匀强电场；在MN的右侧区域，存在着方向竖直向下、磁感应强度为B的匀强磁场，现有一带负电的小球
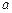从y轴上的P(0，L)点，在电场力作用下由静止开始运动，小球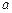到达虚线MN上的Q点时与另一个不带电的静止小球
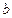发生碰撞，碰后两小球粘合在一起进入磁场，它们穿出磁场的位置恰好在O点．若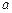、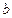两小球的质量相等且均可视为质点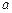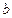，、碰撞过程中无电荷量损失，不计重力作用．求：
（1）小球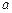的比荷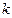
（即电荷量与质量之比）；
（2）过O点后，粘在一起的两个小球再次到达虚线MN上的位置坐标（结果用E、B、L表示）．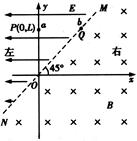
如图所示，质量M="4" kg的滑板B静止放在光滑水平面上，滑板右端固定一根轻质弹簧，弹簧的自由端C到滑板左端的距离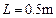
，这段滑板与木块A之间的动摩擦因数
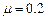，而弹簧自由端C到固定端D所对应的滑板上表面光滑．可视为质点的木块A质量
，原来静止于滑板的左端，滑板B受水平向左恒力F=14N，作用时间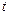
后撤去F，这时木块A恰好到达弹簧自由端C处，假设A、B间的最大静摩擦力和滑动摩擦力相等，
取
，求：
（1）水平恒力F的作用时间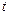
（2）木块A压缩弹簧过程中弹簧的最大弹性势能．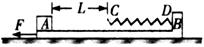
杂技中的“顶竿”由两个演员共同表演，站在地面上的演员肩部顶住一根长竹竿，另一演员爬至竹竿顶端完成各种动作后下滑，若竹竿上演员自竿顶由静止开始下滑，滑到竹竿底部时速度正好为零，已知竹竿底部与下面顶竿人肩部之间有一传感器，传感器显示竿上演员自竿顶滑下过程中顶竿人肩部的受力情况如图所示，竹竿上演员质量为m1=40kg，竹竿质量m2=10kg，g=10m/s2．
（1）求竹竿上的人下滑过程中的最大速度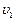
；
（2）请估测竹竿的长度h．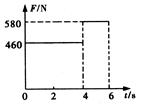
如图所示，水平地面上有一上表面光滑的长木板C(其左端有一竖直小挡板)，其上放有可视为质点的两小物块A和B，其间夹有一根长度可忽略的轻弹簧，弹簧与物块间不相连，其中小物块B距离木板C的右端很近。已知mA=mB="4.0kg," mC=1.0kg地面与木板C间的动摩擦因数为μ=0.20，重力加速度为g=10m/s2。开始时整个装置保持静止，两个小物块A、B将轻质弹簧压紧使弹簧贮存了弹性势能E0=100J。某时刻同时释放A、B，则：
(1)当小物块B滑离木板最右端时，求两小物块的速度魄vA、vB；
(2)若小物块A与挡板的碰撞时间极短且无机械能损失，求在它们第一次碰撞的过程中小物块A对挡板的冲量大小；
(3)在小物块A与挡板第一次碰撞到第二次碰撞的过程中，求木板C的位移大小。
如图所示，在xoy坐标系中，第Ⅲ象限内有场强为E，方向沿x正向的匀强电场，第Ⅱ、Ⅳ象限内有垂直坐标平面向内、强度相等的匀强磁场，第I象限无电、磁场．质量为 m、电量为q的带正电粒子，自x轴上的P点以速度v0垂直电场射入电场中，不计粒子重力和空气阻力，PO之间距离为
(1)求粒子从电场射入磁场时速度的大小和方向．
(2)若粒子由第Ⅳ象限的磁场直接回到第Ⅲ象限的电场中，则磁感应强度大小应满足什么条件?
(3)若磁感应强度
，则粒子从P点出发到第一次回到第Ⅲ象限的电场区域所经历的时间是多少?