如图所示，金属杆
放在光滑的水平金属导轨上，与导轨组成闭合矩形电路，长
宽 
回路总电阻
回路处在竖直向上的磁场中，金属杆用水平绳通过定滑轮连接质量
的木块，磁感应强度从
开始随时间均匀增强，5s末木块将离开水平面，不计一切摩擦，g取
，求回路中的电流强度。
一探照灯照射在云层底面上，这底面是与地面平行的平面，如图所示，云层底面高h，探照灯以匀角速度ω在竖直平面内转动．当光束与竖直线夹角为θ时，求此刻云层底面上光点的移动速度．
如图，以速度v沿竖直杆匀速下滑的物体A，用钢绳通过定滑轮拉物体B在水平面上运动，当绳与水平面夹角为θ时，物体B运动速率为多少？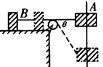
一个质量为0.5kg的物体放在水平面上，它与水平面间的动摩擦因数为μ＝0.2，从静止开始受水平力而运动；物体在前5s内受到一个正东方向、大小为F1＝2.0N的水平恒力作用，在第5s末撤去F1，同时物体进入光滑水平面并受到一个正北方向、大小为F2＝0.5N的水平恒力，作用时间为10s．g＝10m/s2，那么：
（1）该物体在前5s和后10s各做什么运动？
（2）求第5s末和第15s末物体的速度．
一质点做直线运动的
图象如图所示，试分析质点的运动情况，并求出其加速度。
（1）第1 s内；
（2）第1 s末到第3s末；
（3）第4s内。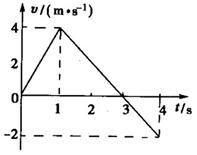
航天飞机以100m/s的速度着陆，在25s内就可停下来，而以8m/s的速度飞行的蜻蜓能在0.7s内停下来，对比它们的速度v、速度的变化量Δv和加速度a的大小？