如图所示是用金属导线制成一矩形框架abcd,其中ab=cd=2ad=2bc=2l=2m,框架放在水平面上,磁感强度为B=1T的匀强磁场垂直于框架平面竖直向下,用同样的金属导线MN垂直于ab和cd,从ad处开始以v0=0.5m/s的速度匀速向右运动,已知该金属导线每米电阻为0.1Ω,求在MN从ad向bc运动的过程中:
(1)MN两点间最大的电势差.
(2)MN运动过程中框架消耗的最大电功率Pm.
右图为东风牌大卡车的远程车灯电路中的蓄电池总功率随电流变化的图象。已知蓄电池瞬间短路时的电流为 30 A。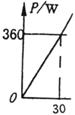
求该蓄电池的电动势ε=?内阻r=?
当内外电阻相等时,蓄电池有最大输出功率.求此功率PM=?
车头两个远程车灯的铭牌上标有“12 V、12 W”字样,若两灯并联接在蓄电池两端,求此时蓄电池输出功率与总功率之比P输出/P总=?
如图所示,R3=8Ω,电源内阻r为2Ω,当S合上且R2为2Ω时,电源的总
功率为24W,而电源的输出功率为16W,灯泡正常发光,求: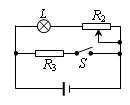
电灯的电阻及功率;
S断开时,为使灯泡正常发光,R2的阻值应调到多少欧?
(选修模块3-5)(15分)下列说法正确的有()
| A.卢瑟福的α粒子散射实验可以估测原子核的大小 |
| B.氢原子辐射出一个光子后,氢原子的电势能增大,核外电子的运动加速度增大 |
| C.物质波是一种概率波,在微观物理学中不可以用“轨迹”来描述粒子的运动 |
| D.若氢原子从 n =" 6" 能级向 n =" 1" 能级跃迁时辐射出的光不能使某金属发生光电效应,则氢原子从 n =" 6" 能级向 n =" 2" 能级跃迁时辐射出的光能使该金属发生光电效应 |
正电子发射计算机断层显象(PET)的基本原理是:将放射性同位素
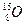 注入人体,
注入人体,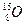 在人体内衰变放出的正电子与人体内的负电子相遇而湮灭,转化为一对γ光子,被探测器探测到,并经计算机处理后产生清晰的图象.根据PET的原理,
在人体内衰变放出的正电子与人体内的负电子相遇而湮灭,转化为一对γ光子,被探测器探测到,并经计算机处理后产生清晰的图象.根据PET的原理,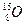 在人体内衰变的方程式是;在PET中,
在人体内衰变的方程式是;在PET中,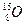 的主要用途是作为.
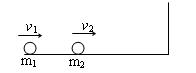
的主要用途是作为.如图所示,质量分别为m1和m2的两个小球在光滑水平面上分别以速度v1、v2同向运动,并发生对心碰撞,碰后m2被右侧墙壁原速率弹回,又与m1碰撞,再一次碰撞后两球都静止.求第一次碰后m1球速度的大小.
(选修模块3-4)(15分)以下说法中正确的是 ( )
| A.拍摄玻璃橱窗内的物品时,往往在镜头前加一个偏振片以增加透射光的强度 |
| B.全息照片往往用激光来拍摄,主要是利用了激光的相干性 |
| C.根据宇宙大爆炸学说,遥远星球发出的红光被地球接收到时可能是红外线 |
| D.超声波可以在真空中传播 |
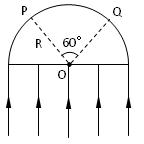
平行光a垂直射向一半径为R的玻璃半球的平面,其截面如图所示,发现只有P、Q之间所对圆心角为60°的球面上有光射出,则玻璃球对a光的折射率为,若仅将a平行光换成b平行光,测得有光射出的范围增大,设a、b两种色光在玻璃球中的速度分别为va和vb,则vavb(选填“>”、“<”或“=”).
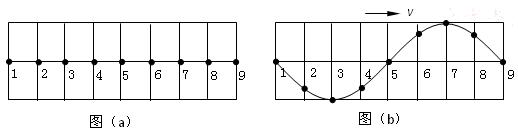
在均匀介质中选取平衡位置在同一直线上的9个质点,相邻两质点间的距离均为0.1m,如图(a)所示.一列横波沿该直线向右传播,t=0时到达质点1,质点1开始向下运动,振幅为0.2m,经过时间0.3s第一次出现如图(b)所示的波形.试写出质点1的振动方程.
如图所示,半径R=0.5m的光滑圆弧面CDM分别与光滑斜面体ABC和斜面MN相切于C、M点,O为圆弧圆心,D为圆弧最低点.斜面体ABC固定在地面上,顶端B安装一定滑轮,一轻质软细绳跨过定滑轮(不计滑轮摩擦)分别连接小物块P、Q (两边细绳分别与对应斜面平行),并保持P、Q两物块静止.若PC间距为L1=0.25m,斜面MN足够长,物块P质量m1= 3kg,与MN间的动摩擦因数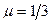 ,求:( sin37°=0.6,cos37°=0.8)
,求:( sin37°=0.6,cos37°=0.8)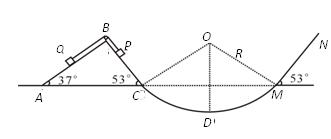
小物块Q的质量m2;
烧断细绳后,物块P第一次到达D点时对轨道的压力大小;
物块P第一次过M点后0.3s到达K点,则 MK间距多大;
物块P在MN斜面上滑行的总路程.