如图所示,在xOy平面上,以y轴上点Ol为圆心,半径为R=0.3m的圆形区域内,分布着一个方向垂直于xOy平面向里,磁感应强度大小为B=0.5T的匀强磁场。一个比荷 的带正电粒子,从磁场边界上的原点O,以
的带正电粒子,从磁场边界上的原点O,以 的初速度,沿不同方向射入磁场,粒子重力不计,求:
的初速度,沿不同方向射入磁场,粒子重力不计,求: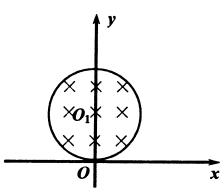
(1)粒子在磁场中运动的轨道半径;
(2)粒子通过磁场空间的最长运动时间。
(8分)一宠物毛毛狗“乐乐”在玩耍时不慎从离地h1=19.5m高层阳台无初速度竖直掉下,当时刚好是无风天气,设它的质量m=2kg,在“乐乐”开始掉下的同时,几乎在同一时刻刚好被地面上的一位保安发现并奔跑到达楼下,奔跑过程用时2.5s,恰好在距地面高度为h2=1.5m处接住“乐乐”, “乐乐”缓冲到地面时速度恰好为零,设“乐乐”下落过程中空气阻力为其重力的0.6倍,缓冲过程中空气阻力为其重力的0.2倍,重力加速度g=10m/s2。求:
(1)为了营救“乐乐”允许保安最长的反应时间;
(2)在缓冲过程中保安对“乐乐”做的功。
如图所示,一只小球用绳OA和OB拉住,OA水平,OB与水平方向成60°角,这时OB绳受的拉力为8 N,求小球重力及OA绳拉力的大小.
图2-6-21
如图所示,两根相同的橡皮绳OA、OB,开始夹角为0°,在O点处打结吊一重50 N的物体后,结点O刚好位于圆心.今将A、B分别沿圆周向两边移至A′、B′, 使∠AOA′=∠BOB′=60°,欲使结点仍在圆心处,则此时结点处应挂多重的物体?
使∠AOA′=∠BOB′=60°,欲使结点仍在圆心处,则此时结点处应挂多重的物体?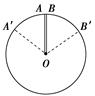
图2-5-19
.在东北的冬季伐木工作中,被伐下的木料常装在钢制滑板上的雪橇上,马拉着雪橇在冰道上滑行,将木料运出,如图2-4-18.在水平冰道上,马在水平方向的最大拉力为1000 N,能够长时间拉着一雪橇匀速前进,马最多能拉多重的木材才能在水平冰道上较长时间匀速前进呢?(已知雪橇及人的总重量为1800 N,雪橇与冰面之间的动摩擦因数为0.02)
图2-4-18
从跳高运动史看,100年内跳高的姿势发生了五次变革,跨越式、剪式、滚式、俯卧式、背越式五种.每改革一次姿势,跳高的世界纪录就提高一次.1 .70 m的第一个世界纪录是用跨越式创造的;第二届奥运会上,巴克斯捷尔用剪式越过1.90 m的横杆;1912年美国运动员霍林用滚式创造了2.01 m的好成绩;29年以后美国运动员用俯卧式以2.11 m的成绩创造了新的世界纪录.现代新的姿势是背越式,背越式出现以后,跳高的成绩更加提高了,1984年我国运动员朱建华创造的世界纪录为2.30 m.1993年古巴运动员索托马约尔创造了2.43 m的世界纪录,现在各国的优秀跳高运动员都在力争创造更高的世界纪录.
.70 m的第一个世界纪录是用跨越式创造的;第二届奥运会上,巴克斯捷尔用剪式越过1.90 m的横杆;1912年美国运动员霍林用滚式创造了2.01 m的好成绩;29年以后美国运动员用俯卧式以2.11 m的成绩创造了新的世界纪录.现代新的姿势是背越式,背越式出现以后,跳高的成绩更加提高了,1984年我国运动员朱建华创造的世界纪录为2.30 m.1993年古巴运动员索托马约尔创造了2.43 m的世界纪录,现在各国的优秀跳高运动员都在力争创造更高的世界纪录.
图2-1-8
跳高姿势的变化是不断刷新跳高成绩的关键之一,但是在姿势的变化中包含着哪些物理原理呢?