在真空室内取坐标系xOy，在x轴上方存在两个方向都垂直于纸面向外的磁场区Ⅰ和II（如图），平行于x轴的虚线MM’和NN’是它们的边界线，两个区域在y方向上的宽度都为d、在x方向上都足够长．Ⅰ区和II区内分别充满磁感应强度为B和
的匀强磁场．一带正电的粒子质量为m、电荷量为q，从坐标原点O以大小为v的速度沿y轴正方向射入Ⅰ区的磁场中．不计粒子的重力作用．
（1）如果粒子只是在Ⅰ区内运动而没有到达II区，那么粒子的速度v满足什么条件？粒子运动了多长时间到达x轴？
（2）如果粒子运动过程经过II区而且最后还是从x轴离开磁场，那么粒子的速度v又满足什么条件？并求这种情况下粒子到达x轴的坐标范围？
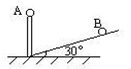
如图，A、B两小球带等量同号电荷，A固定在竖直放置的10cm长的绝缘支杆上，B平衡于光滑的绝缘斜面上与A等高处，斜面倾角为30°，B的质量为52g，求B的带电量．
如图所示，A、B为体积可忽略的带电小球，QA＝2×10-8C，QB＝－2×10-8C，A、B相距3cm．在水平外电场作用下，A、B保持静止，悬线都沿竖直方向．试求：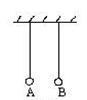
（1）外电场的场强大小和方向？（2）AB中点处总电场的场强大小和方向．
设氢原子核外电子的轨道半径为r，电子质量为m，电量为e，求电子绕核运动的周期．
大小相同的金属小球，所带电量的值分别为Q1、Q2，且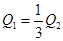
,把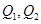
放在相距较远的两点，他们间作用力的大小为F，若使两球相接触后再分开放回原位置，求它们间作用力的大小．
有两个完全相同的带电绝缘金属小球A、B，分别带有电荷量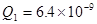
C，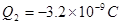
，让两绝缘金属小球接触，在接触的过程中，电子如何转移并转移了多少？