如图所示，质量为m、电荷量为+q的粒子从坐标原点Ｏ以初速度v0射出，粒子恰好经过A点，Ｏ、A两点长度为l ，连线与坐标轴＋y方向的夹角为
= 370，不计粒子的重力．
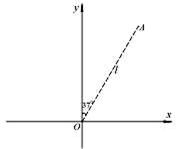
（1）若在平行于x轴正方向的匀强电场E１中，粒子沿＋y方向从O点射出，恰好经过A点；若在平行于y轴正方向的匀强电场E２中，粒子沿＋x方向从O点射出，也恰好能经过A点，求这两种情况电场强度的比值
．
（2）若在y轴左侧空间（第Ⅱ、Ⅲ象限）存在垂直纸面的匀强磁场，粒子从坐标原点O，沿与＋y轴成300的方向射入第二象限，恰好经过A点，求磁感应强度B．
如下图所示，质量为40.0kg的雪橇（包括人）在与水平方向成37°角、大小为200N的拉力F作用下，沿水平面由静止开始运动，雪橇与地面间动摩擦因数为0.20；取g=10m/s2，cos37°=0.8，sin37°=0.6。求雪橇的加速度大小；
经过2s撤去F，再经过3s时雪橇的速度多大？
雪橇在5s内的位移多大？
许多汽车司机喜欢在驾驶室悬挂一些祝福“平安”的小工艺品。如下图所示，沿水平方向做匀变速直线运动的车厢中，悬挂小工艺品的悬线偏离竖直方向37°角，球和车厢相对静止，球的质量为1kg。（g＝10m/s2，sin37°＝0.6，cos37°＝0.8）求车厢运动的加速度，并说明车厢的运动情况；
求悬线对球的拉力。
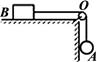
在水平地面上放一木板B，重力为G2=100N，再在木板上放一货箱A，重力为G1=500N，设货箱与木板、木板与地面的动摩擦因数μ均为0.5，先用绳子把货箱与墙拉紧，如下图所示，已知sinθ=0.6，cosθ=0.8，然后在木板B上施一水平力F，想把木板从货箱下抽出来，F至少应为多大？
如下图所示，贴着竖直墙面的物体A的质量mA=0.2kg，放在水平面上的物体B的质量mB=1.0kg，绳和滑轮间的摩擦均不计，且绳的OB部分水平，OA部分竖直，A和B恰好一起匀速运动。取g=10m/s2，求：物体B与桌面间的动摩擦因数？
如果用水平力F向左拉B，使物体A和B做匀速运动，需多大的拉力？
若在原来静止的物体B上放一个质量与B物体质量相等的物体后，物体B受到的摩擦力多大？
如下图所示，质量
kg的木块A套在水平杆上，并用轻绳将木块与质量
kg的小球B相连。今用跟水平方向成α=30°角的力
N，拉着球带动木块一起向右匀速运动，运动中M、m相对位置保持不变，取g=10m/s2。求：运动过程中轻绳与水平方向夹角θ；
木块与水平杆间的动摩擦因数μ。
当
为多大时，使球和木块一起向右匀速运动的拉力最小？