如图:已知在正方形ABCD中,E是边AB的中点,点F在BC上,且∠ADE=∠FDE。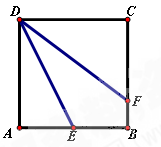
(1)求证:DF=AB+FB;
(2)以E为圆心EB为半径作⊙E,试判断⊙E与直线DF的位置关系,并说明理由;
(3)在⑵的条件下,若CD=4cm,点M在线段DF上从点D出发向点F运动,速度为0.5cm/s,以M为圆心,MD为半径作⊙M。当运动时间为多少秒时,⊙M与⊙E相切?
某超市今年2月份的销售收入比1月份有所下降.3月份的销售收入比1月份的销售收入增长了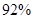 ,且比2月份的销售收入翻了一番.
,且比2月份的销售收入翻了一番.求该超市今年2月份的销售收入比1月份下降了百分之几
若该超市今年1~3月份每月的销售分别获得了
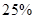 、
、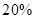 、
、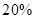 的利润,求该超市今年第一季度销售的利润率.(
的利润,求该超市今年第一季度销售的利润率.(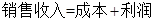 ,
, )
)
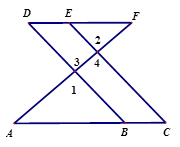
如图,点 在
在 上,点
上,点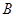 在
在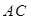 上,
上,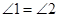 ,
,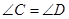 .
.
试说明: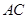 ∥
∥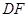 .将过程补充完整.
.将过程补充完整.
解:∵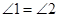 (已知)
(已知)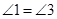 ()
()
∴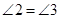 (等量代换)
(等量代换)
∴ ∥()
∴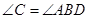 ()
()
又∵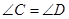 (已知)
(已知)
∴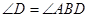 ()
()
∴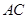 ∥
∥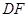 ()
()
今年植树节,我市 中学的同学们都参加了植树活动,其中七年级植树200棵.小聪用扇形统计图统计了今年植树三个年级所占百分比的情况,如图1所示. 小明用象形统计图对各年级的植树情况进行了统计,如图2所示.
中学的同学们都参加了植树活动,其中七年级植树200棵.小聪用扇形统计图统计了今年植树三个年级所占百分比的情况,如图1所示. 小明用象形统计图对各年级的植树情况进行了统计,如图2所示.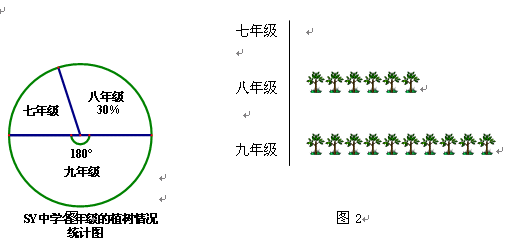
根据以上信息,解决下列问题:七年级今年植树棵数占三个年级植树棵数的百分比是多少?
三个年级今年一共植树多少棵?
指出图2的象形统计图中的每一个
 的含义;
的含义;补全图2中的象形统计图
如图,在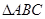 中,延长
中,延长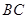 至
至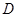 ,
,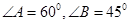 .
.过点
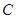 作直线
作直线 ∥
∥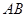 (尺规作图,不写作法,保留作图痕迹);
(尺规作图,不写作法,保留作图痕迹);求
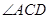 的度数
的度数
某同学在计算一个多项式乘以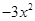 时,因抄错运算符号,算成了加上
时,因抄错运算符号,算成了加上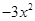 ,得到的结果是
,得到的结果是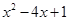 ,那么正确的计算结果是多少?
,那么正确的计算结果是多少?