满足a,b∈{-1,0,1,2},且关于x的方程ax2+2x+b=0有实数解的有序数对(a,b)的个数为( ).
| A.14 | B.13 |
| C.12 | D.10 |
某人射击一次击中目标的概率为0.6,经过3次射击,此人至少有2次击中目标的概率为()
七人并排站成一行,如果甲、乙两人必需不相邻,那么不同的排法的种数是()
| A.1440 | B.3600 | C.4320 | D.4800 |
设f(x)是(-∞,∞)是的奇函数,f(x+2)=-f(x),当0≤x≤1时,f(x)=x,则f(7.5)等于()
| A.0.5 | B.-0.5 | C.1.5 | D.-1.5 |
若sin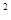 x>cos
x>cos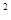 x,则x的取值范围是()
x,则x的取值范围是()
A.{x|2k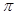 - -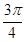 <x<2k <x<2k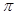 + +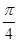 ,k ,k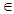 Z} Z} |
B.{x|2k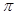 + +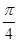 <x<2k <x<2k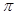 + +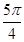 ,k ,k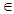 Z} Z} |
C.{x|k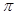 - -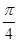 <x<k <x<k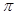 + +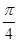 ,k ,k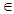 Z } Z } |
D.{x|k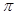 + +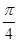 <x<k <x<k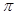 + +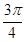 ,k ,k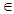 Z} Z} |
椭圆mx2+ny2=1与直线x+y=1交于A、B两点,过AB中点M与原点的直线斜率为 ,则
,则 的值为()
的值为()
A. B.
B. C.1 D.
C.1 D.