如图,在平面直角坐标系xOy中,椭圆C: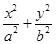 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,以坐标原点为圆心,椭圆C的短半轴长为半径的圆与直线x-y+2=0相切.
,以坐标原点为圆心,椭圆C的短半轴长为半径的圆与直线x-y+2=0相切.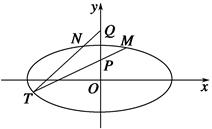
(1)求椭圆C的方程;
(2)已知点P(0,1),Q(0,2),设M,N是椭圆C上关于y轴对称的不同两点,直线PM与QN相交于点T.求证:点T在椭圆C上.
设数列 的前项n和为
的前项n和为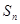 ,若对于任意的正整数n都有
,若对于任意的正整数n都有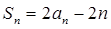 .
.
(1)设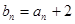 ,求证:数列
,求证:数列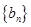 是等比数列,
是等比数列,
(2)求证: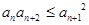
(3)求数列 的前n项和
的前n项和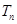 .
.
如图,在△ABC中已知∠B=60°,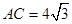 ,D是BC边上的一点.
,D是BC边上的一点.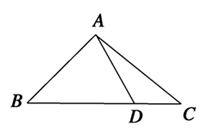
(1)若AD=2,在△ACD的面积S=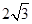 ,求CD的长.
,求CD的长.
(2)若AB=AD,试求△ACD面积S的最大值.
某公司计划2015年在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元.甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟,假定甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元,问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大?最大收益是多少万元?
(1)解关于 不等式
不等式 .
.
(2)证明: (其中
(其中 ).
).
已知等差数列 的前n项和为
的前n项和为 ,且
,且 ,
,
(1)求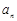 ;
;
(2)求 的最大值.
的最大值.