一列波以60°入射角入射到两种介质的交界面,反射波刚好与折射波垂直.若入射波的波长为0.6 m,那么折射波的波长为多少?反射波的波长为多少?
在水平光滑的绝缘桌面内建立如图所示的直角坐标系xOy,将第1、II象限称为区域一,第Ⅲ、Ⅳ象限称为区域二,其中一个区域内有匀强电场,另一个区域内有大小为2×10-2T、方向垂直桌面的匀强磁场,把一个比荷为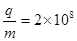 C/kg的正电荷从坐标为(0,-1)的A点处由静止释放,电荷以一定的速度从坐标为(1,0)的C点第一次经x轴进入区域一,经过一段时间,从坐标原点O再次回到区域二.
C/kg的正电荷从坐标为(0,-1)的A点处由静止释放,电荷以一定的速度从坐标为(1,0)的C点第一次经x轴进入区域一,经过一段时间,从坐标原点O再次回到区域二.
(1)指出哪个区域存在电场、哪个区域存在磁场,以及电场和磁场的方向.
(2)求电场强度的大小.
(3)求电荷第三次经过x轴的位置.
一物体在某一时刻以一定的初速度v0开始作匀变速直线运动,已知物体在第3s内的位移是7.5m,在第6、第7两秒内的位移是8m,求物体运动的初速度v0及加速度a?
如图所示,真空中有一以(r,0)为圆心、半径为r的圆柱形匀强磁场区域,磁场的磁感强度大小为B,方向垂直纸面向里.磁场的上方有两等大的平行金属板MN,两板间距离为2r.从O点向不同方向发射速率相同的质子,质子的运动轨迹均在纸面内.当质子进入两板间时两板间可立即加上如图所示的电压,且电压从t=0开始变化,电压的最大值为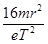 ,已知质子的电荷量为e,质量为m,质子在磁场中的偏转半径也为r,不计重力,求:
,已知质子的电荷量为e,质量为m,质子在磁场中的偏转半径也为r,不计重力,求:
(1)质子进入磁场时的速度大小;
(2)若质子沿x轴正方向射入磁场,到达M板所需的时间为多少?
(3)若质子沿与x轴正方向成某一角度θ的速度射入磁场时,粒子离开磁场后能够平行于金属板进入两板间,求θ的范围以及质子打到M板时距坐标原点O的距离。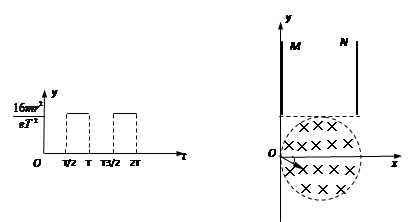
如图所示, AB段为一半径R=0.2m的光滑 圆形轨道,EF为一倾角为30°的光滑斜面,斜面上有一质量为0.1Kg的薄木板CD, 木板的下端D离斜面底端的距离为15m,开始时木板被锁定.一质量也为0.1Kg的物块从A点由静止开始下滑,通过B点后被水平抛出,经过一段时间后恰好以平行于薄木板的方向滑上木板,在物块滑上木板的同时木板解除锁定.已知物块与薄木板间的动摩擦因数为
圆形轨道,EF为一倾角为30°的光滑斜面,斜面上有一质量为0.1Kg的薄木板CD, 木板的下端D离斜面底端的距离为15m,开始时木板被锁定.一质量也为0.1Kg的物块从A点由静止开始下滑,通过B点后被水平抛出,经过一段时间后恰好以平行于薄木板的方向滑上木板,在物块滑上木板的同时木板解除锁定.已知物块与薄木板间的动摩擦因数为 .取g=10m/s2,求:
.取g=10m/s2,求:
⑴物块到达B点时对圆形轨道的压力大小;
⑵物块做平抛运动的时间;
⑶若下滑过程中某时刻物块和木板达到共同速度,则这个速度为多大?
一艘小艇从河岸上的A处出发渡河,小艇艇身保持与河岸垂直,经过t1=10min,小艇到达正对岸下游x=120m的C处,如图所示,如果小艇保持速度大小不变逆水斜向上游与河岸成角方向行驶,则经过t2=12.5min,小艇恰好到达河对岸的B处。求: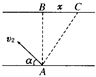
(1)水流的速度;
(2)船在静水中的速度;
(3)河宽;
(4)船头与河岸的夹角。