根据如图示的振动图像.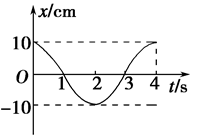
(1)算出下列时刻振子对应平衡位置的位移.
①t1=0.5 s;②t2=1.5 s.
(2)将位移随时间的变化规律写成x=Asin(ωt+φ)的形式并指出振动的初相位是多少?
如图,竖直放置的斜面AB的下端与光滑的圆弧轨道BCD的B端相切,C为圆弧最低点,圆弧半径为R,圆心O与A、D在同一水平面上,∠ COB=30°。现有一个质量为m的小物体从A点无初速滑下,已知小物体与斜面间的动摩擦因数为m,
求:(1)小物体在斜面上滑行的总路程;
(2)小物体通过C点时,对C点的最大压力和最小压力。
一宇航员在某一行星极地着陆后,发现自己在当地重力是地球上重力的 ,进一步研究还发现,该行星一昼夜的时间与地球相同,而且物体在行星赤道上对行星无压力,求出该行星的半径.(已知地球自转周期为T,地球表面重力加速度为g)
,进一步研究还发现,该行星一昼夜的时间与地球相同,而且物体在行星赤道上对行星无压力,求出该行星的半径.(已知地球自转周期为T,地球表面重力加速度为g)
如图所示,一条光线从空气中垂直射到棱镜界面BC上,棱镜的折射率为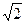 ,这条光线离开棱镜时与界面的夹角可为多少度?
,这条光线离开棱镜时与界面的夹角可为多少度?
一火箭喷气发动机每次喷出m=2000g的气体,喷出气体相对地面速度v="100" m/s。若此火箭初始总质量M=300kg,发动机每秒喷气20次,不考虑地球引力及空气阻力的情况下,火箭发动机1s末的速度是多大?
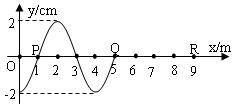
一列沿x轴正方向传播的简谐波,在t=0时刻的波的图像如图所示。已知这列波在P出现两次波峰的最短时间是0.4s,求:
(1)这列波的波速v是多少?
(2)再经过多长时间R才能第一次到达波峰?
(3)这段时间里R通过的路程是多少