某高中为了推进新课程改革,满足不同层次学生的需求,决定从高一年级开始,在每周的周一、周三、周五的课外活动期间同时开设数学、物理、化学、生物和信息技术辅导讲座,每位有兴趣的同学可以在期间的任何一天参加任何一门科目的辅导讲座,也可以放弃任何一门科目的辅导讲座。(规定:各科达到预先设定的人数时称为满座,否则称为不满座)统计数据表明,各学科讲座各天的满座的概率如下表: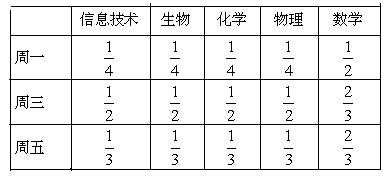
根据上表:
(1)求数学辅导讲座在周一、周三、周五都不满座的概率;
(2)设周三各辅导讲座满座的科目数为 ,求随机变量
,求随机变量 的分布列和数学期望。
的分布列和数学期望。
已知:函数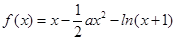 ,其中
,其中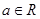 .
.
(Ⅰ)若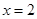 是
是 的极值点,求
的极值点,求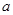 的值;
的值;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)若 在
在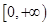 上的最大值是
上的最大值是 ,求
,求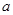 的取值范围.
的取值范围.
某商场销售某种商品的经验表明,该商品每日的销售量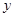 (单位:千克)与销售价格
(单位:千克)与销售价格 (单位:
(单位:
元/千克)满足关系式 .其中
.其中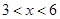 ,
,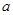 为常数.已知销售价格为
为常数.已知销售价格为 元/千克时,每
元/千克时,每
日可售出该商品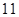 千克.
千克.
(Ⅰ)求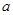 的值;
的值;
(Ⅱ)若该商品的成本为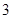 元/千克,试确定销售价格
元/千克,试确定销售价格 的值,使商场每日销售该商品所获得的利润最大.
的值,使商场每日销售该商品所获得的利润最大.
甲、乙两支球队进行总决赛,比赛采用七场四胜制,即若有一队先胜四场,则此队为总冠军,比赛就此结束.因两队实力相当,每场比赛两队获胜的可能性均为二分之一.据以往资料统计,第一场比赛可获得门票收入 万元,以后每场比赛门票收入比上一场增加
万元,以后每场比赛门票收入比上一场增加 万元.
万元.
(Ⅰ)求总决赛中获得门票总收入恰好为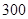 万元的概率;
万元的概率;
(Ⅱ)设总决赛中获得的门票总收入为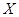 ,求
,求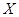 的分布列.
的分布列.
当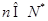 时,
时, ,
,
(Ⅰ)求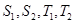 ;
;
(Ⅱ)猜想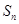 与
与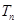 的关系,并用数学归纳法证明.
的关系,并用数学归纳法证明.
已知 ,且
,且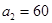 .
.
(Ⅰ)求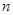 的值;
的值;
(Ⅱ)求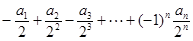 的值.
的值.