已知函数f(x)=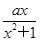 +a,g(x)=aln x-x(a≠0).
+a,g(x)=aln x-x(a≠0).
(1)求函数f(x)的单调区间;
(2)求证:当a>0时,对于任意x1,x2∈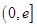 ,总有g(x1)<f(x2)成立.
,总有g(x1)<f(x2)成立.
已知命题p:“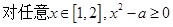 ”,命题q:“
”,命题q:“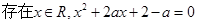 ”若命题“p且q”是真命题,求实数a的取值范围.
”若命题“p且q”是真命题,求实数a的取值范围.
已知椭圆 过点
过点 ,其长轴、焦距和短轴的长的平方依次成等差数列.
,其长轴、焦距和短轴的长的平方依次成等差数列.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)若直线与 轴正半轴、
轴正半轴、 轴分别交于点
轴分别交于点 ,与椭圆分别交于点
,与椭圆分别交于点 ,各点均不重合,且满足
,各点均不重合,且满足 ,
, . 当
. 当 时,试证明直线过定点.过定点(1,0)
时,试证明直线过定点.过定点(1,0)
已知 .
.
(Ⅰ) 时,求证
时,求证 在
在 内是减函数;
内是减函数;
(Ⅱ)若 在
在 内有且只有一个极值点,求实数
内有且只有一个极值点,求实数 的取值范围.
的取值范围.
已知等差数列 ,公差
,公差 ,前
,前 项和为
项和为 ,且满足
,且满足 ,
, .
.
(Ⅰ)求数列 的通项公式及前
的通项公式及前 项和
项和
(Ⅱ)设 ,若数列
,若数列 也是等差数列,试确定非零常数
也是等差数列,试确定非零常数 ,并求数列
,并求数列 的前
的前 项和
项和 .
.
如图所示,已知圆 的直径
的直径 长度为4,点
长度为4,点 为线段
为线段 上一点,且
上一点,且 .点
.点 为圆
为圆 上一点,且
上一点,且 .点
.点 在圆
在圆 所在平面上的射影为点
所在平面上的射影为点 ,
, .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求 与平面
与平面 所成的角的正弦值。
所成的角的正弦值。