设f(x)= +xln x,g(x)=x3-x2-3.
+xln x,g(x)=x3-x2-3.
(1)如果存在x1,x2∈[0,2]使得g(x1)-g(x2)≥M成立,求满足上述条件的最大整数M;
(2)如果对于任意的s,t∈ ,都有f(s)≥g(t)成立,求实数a的取值范围.
,都有f(s)≥g(t)成立,求实数a的取值范围.
函数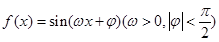 ,在同一个周期内,当
,在同一个周期内,当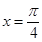 时
时 取最大值1,当
取最大值1,当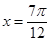 时,
时, 取最小值-1
取最小值-1
(1)求函数的解析式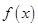 ;
;
(2)若函数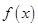 满足方程
满足方程 ;求在
;求在 内的所有实数根之和.
内的所有实数根之和.
在人群流量较大的街道,有一中年人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、3只白色的乒乓球(其体积、质地完成相同),旁边立着一块小黑板写道:
摸球方法:从袋中随机摸出3个球,若摸得同一颜色的3个球,摊主送给摸球者5元钱;若摸得非同一颜色的3个球,摸球者付给摊主1元钱。
(1)摸出的3个球为白球的概率是多少?
(2)摸出的3个球为2个黄球1个白球的概率是多少?
(3)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一个月(按30天计)能赚多少钱?
已知函数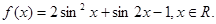
(1)求 的最小正周期及
的最小正周期及 取得最大值时x的集合;
取得最大值时x的集合;
(2)在平面直角坐标系中画出函数 在
在 上的图象.
上的图象.
已知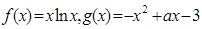
(1)求函数 在
在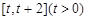 上的最小值
上的最小值
(2)对一切的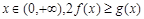 恒成立,求实数a的取值范围
恒成立,求实数a的取值范围
(3)证明对一切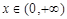 ,都有
,都有 成立
成立
已知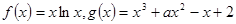
(Ⅰ)如果函数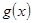 的单调递减区间为
的单调递减区间为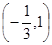 ,求函数
,求函数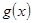 的解析式;
的解析式;
(Ⅱ)对一切的 ,
,
 恒成立,求实数
恒成立,求实数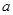 的取值范围
的取值范围