已知等差数列{an}的公差不为零,a1=25,且a1,a11,a13成等比数列.
(1)求{an}的通项公式;
(2)求a1+a4+a7+…+a3n-2.
在平面直角坐标系
中,点
到点
的距离比它到
轴的距离多1,记点
的轨迹为
.
(1)求轨迹为
的方程;
(2)设斜率为
的直线
过定点
,求直线
与轨迹
恰好有一个公共点,两个公共点,三个公共点时
的相应取值范围.
计划在某水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水库年入流量
(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(1)求未来4年中,至多1年的年入流量超过120的概率;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量
限制,并有如下关系:
| 年入流量 | |||
| 发电量最多可运行台数 |
1 |
2 |
3 |
若某台发电机运行,则该台年利润为5000万元;若某台发电机未运行,则该台年亏损800万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
如图,在棱长为2的正方体 中, 分别是棱 的中点,点 分别在棱 上移动,且 .
(1)当 时,证明:直线 平面 ;
(2)是否存在
,使平面
与面
所成的二面角为直二面角?若存在,求出
的值;若不存在,说明理由.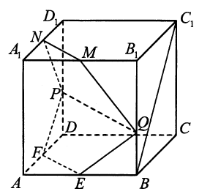
已知等差数列 满足: ,且 .
(1)求数列
的通项公式.
(2)记
为数列
的前
项和,是否存在正整数
,使得
若存在,求
的最小值;若不存在,说明理由.
某实验室一天的温度(单位:
)随时间
(单位:
)的变化近似满足函数关系;
.
(1)求实验室这一天的最大温差;
(2)若要求实验室温度不高于11
,则在哪段时间实验室需要降温?