若函数f(x)=log3(x2-2ax+5)在区间(-∞,1]上单调递减,则a的取值范围是( )
| A．[1,+∞) | B．(1,+∞) |
| C．[1,3) | D．[1,3] |
观察下列各式:72=49,73=343,74=2401,…,则72011的末两位数字为( )
| A．01 | B．43 |
| C．07 | D．49 |
观察下列事实:|x|+|y|=1的不同整数解(x,y)的个数为4,|x|+|y|=2的不同整数解(x,y)的个数为8,|x|+|y|=3的不同整数解(x,y)的个数为12,…,则|x|+|y|=20的不同整数解(x,y)的个数为( )
| A．76 | B．80 |
| C．86 | D．92 |
对于函数y=f(x)(x∈I),y=g(x)(x∈I),若对任意x∈I,存在x0使得f(x)≥f(x0),g(x)≥g(x0)且f(x0)=g(x0),则称f(x),g(x)为“兄弟函数”,已知f(x)=x2+px+q,g(x)=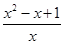
是定义在区间
上的“兄弟函数”,那么函数f(x)在区间上的最大值为( )
A． |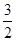
B．2 | C．4 | D． |
在实数的原有运算法则中,我们补充定义新运算“⊕”;当a≥b时,a⊕b=a;当a<b时,a⊕b=b2,函数f(x)=(1⊕x)·x(其中“·”仍为通常的乘法),则函数f(x)在[0,2]上的值域为( )
| A．[0,4] | B．[1,4] | C．[0,8] | D．[1,8] |
函数y=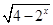
的值域是( )
| A．[0,+∞) | B．[0,2] |
| C．[0,2) | D．(0,2) |