设函数f(x)=g(x)+x2,曲线y=g(x)在点(1,g(1))处的切线方程为y=2x+1,则曲线y=f(x)在点(1,f(1))处的切线的斜率为( )
| A．2 | B．- |
C．4 | D．- |
一个总体共有600个个体，随机编号为001，002，… ，600．采用系统抽样的方法抽取一个容量为50的样本，且随机抽得的号码为003．这600个个体分三组，从001到300在第1组，从301到495在第2组，从496到600在第3组．则第3组被抽中的个数为 （）
| A．7 | B． 8 | C．9 | D．10 |
已知数列{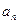
}(n=
)满足
,且当
时,
. 若
, 
，则符合条件的数列{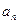}的个数是（）
| A．140 | B．160 | C．840 | D．5040 |
在(0,
)内，使
成立的
的取值范围为（）
A．[ ] |
B．[ ] |
C．[ ] |
D．[ ] |
过点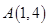
，且横、纵截距的绝对值相等的直线的条数为（）
| A．1 | B． 2 | C．3 | D．4 |
在各项均为实数的等比数列
中，
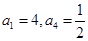，则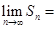
（）
| A．2 | B． 8 | C．16 | D．32 |