已知{an}是各项均为正数的等比数列,且a1+a2=2( +
+ ),a3+a4+a5=64(
),a3+a4+a5=64( +
+ +
+ ),
),
(1)求{an}的通项公式.
(2)设bn=(an+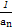 )2,求数列{bn}的前n项和Tn.
)2,求数列{bn}的前n项和Tn.
(本小题满分13分)某同学用“五点法”画函数 (
(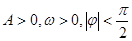 )在某一个周期内的图像时,列表并填入的部分数据如下表:
)在某一个周期内的图像时,列表并填入的部分数据如下表:
 |
 |
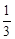 |
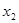 |
 |
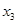 |
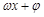 |
 |
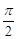 |
 |
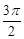 |
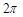 |
 |
 |
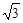 |
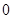 |
 |
 |
(1)请求出上表中的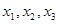 的值,并写出函数
的值,并写出函数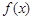 的解析式;
的解析式;
(2)将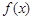 的图像向右平移
的图像向右平移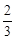 个单位得到函数
个单位得到函数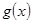 的图像,若函数
的图像,若函数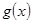 在区间
在区间 (
(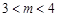 )上的图像的最高点和最低点分别为
)上的图像的最高点和最低点分别为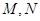 ,求向量
,求向量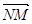 与
与 夹角
夹角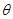 的大小.
的大小.
(本小题满分13分)甲、乙两支篮球队赛季总决赛采用7场4胜制,每场必须分出胜负,场与场之间互不影响,只要有一队获胜4场就结束比赛.现已比赛了4场,且甲篮球队胜3场.已知甲球队第5,6场获胜的概率均为 ,但由于体力原因,第7场获胜的概率为
,但由于体力原因,第7场获胜的概率为 .
.
(1)求甲队分别以 ,
, 获胜的概率;
获胜的概率;
(2)设X表示决出冠军时比赛的场数,求X的分布列及数学期望.
(本小题满分10分)设不等式 的解集为
的解集为 , 且
, 且 .
.
(Ⅰ)试比较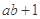 与
与 的大小;
的大小;
(Ⅱ)设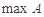 表示数集
表示数集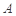 中的最大数, 且
中的最大数, 且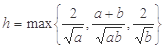 , 求
, 求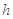 的范围.
的范围.
(本小题满分10分)已知直线l的参数方程是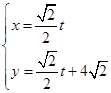 (t是参数),圆C的极坐标方程为
(t是参数),圆C的极坐标方程为 .
.
(Ⅰ)求圆心C的直角坐标;
(Ⅱ)由直线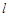 上的点向圆C引切线,求切线长的最小值.
上的点向圆C引切线,求切线长的最小值.
(本小题满分10分)如图,已知PA与圆O相切于点A,经过点O的割线PBC交圆O于点B、C,∠APC的平分线分别交AB、AC于点D、E,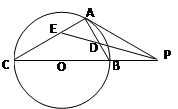
(Ⅰ)证明:∠ADE=∠AED;
(Ⅱ)若AC=AP,求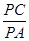 的值.
的值.