如图所示,面积为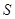 的平面凸四边形的第
的平面凸四边形的第 条边的边长记为
条边的边长记为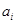 (
(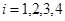 ),此四边形内任一点
),此四边形内任一点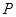 到第
到第 条边的距离记为
条边的距离记为 (
(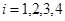 ),若
),若 ,则
,则 .类比以上性质,体积为
.类比以上性质,体积为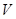 的三棱锥的第
的三棱锥的第 个面的面积记为
个面的面积记为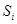 (
(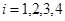 ),此三棱锥内任一点
),此三棱锥内任一点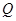 到第
到第 个面的距离记为
个面的距离记为 (
(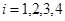 ),若
),若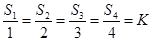 ,则
,则 等于()
等于()
A. |
B. |
C. |
D. |
若变量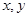 满足
满足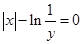 ,则
,则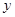 关于
关于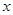 的函数图象大致是()
的函数图象大致是()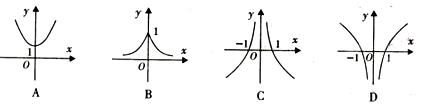
给出下列四个命题:
①使用 统计量作
统计量作 列联表的独立性检验时,要求表中的4个数据都要大于10;
列联表的独立性检验时,要求表中的4个数据都要大于10;
②使用 统计量进行独立性检验时,若
统计量进行独立性检验时,若 ,则有
,则有 的把握认为两个事件有关;
的把握认为两个事件有关;
③回归直线就是散点图中经过样本数据点最多的那条直线
④在线性回归分析中,如果两个变量的相关性越强,则相关系数 就越接近于1.
就越接近于1.
其中真命题的个数为()
| A.1个 | B.2个 | C.3个 | D.4个 |
设点P是函数 图象上异于原点的动点,且该图象在点P处的切线的
图象上异于原点的动点,且该图象在点P处的切线的
倾斜角为 ,则
,则 的取值范围是()
的取值范围是()
A. |
B. |
C. |
D. |
若大前提是:任何实数的平方都大于0,小前提是: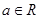 ,结论是:
,结论是: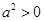 ,那么这个演绎推理()
,那么这个演绎推理()
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.没有错误 |