袋内装有6个球,这些球依次被编号为1、2、3、……、6,设编号为n的球重n2-6n+12(单位:克),这些球等可能地从袋里取出(不受重量、编号的影响).
(1)从袋中任意取出一个球,求其重量大于其编号的概率;
(2)如果不放回地任意取出2个球,求它们重量相等的概率.
(本小题满分16分,每小题8分)
解下列不等式:
(1)  ; (2) log73x < log7(x2-4).
; (2) log73x < log7(x2-4).
(本小题满分14分)
已知函数f(x)=log2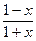 .
.
(1)判断并证明f(x)的奇偶性;
(2)若关于x的方程f(x)=log2(x-k)有实根,求实数k的取值范围;
(3)问:方程f(x)=x+1是否有实根?如果有,设为x0,请求出一个长度
为 的区间(a,b),使x0∈(a,b);如果没有,请说明理由.
的区间(a,b),使x0∈(a,b);如果没有,请说明理由.
(注:区间(a,b)的长度为b-a)
(本小题满分12分)
已知集合A={x|log2(x-1)<1},集合B={x|x2-ax+b<0,a,b∈R}.
(1)若A=B,求a,b的值;
(2)若b=3,且A∪B=A,求a的取值范围.
(本小题满分12分)
已知函数f(x)=2x的定义域是[0,3],设g(x)=f(2x)-f(x+2).
(1)求g(x)的解析式及定义域;
(2)求函数g(x)的最大值和最小值.
(本小题满分12分)
目前,成都市B档出租车的计价标准是:路程2 km以内(含2 km)按起步价8元 收取,超过2 km后的路程按1.9元/km收取,但超过10 km后的路程需加收50%的返空费(即单价为1.9×(1+50%)=2.85元/km).
收取,超过2 km后的路程按1.9元/km收取,但超过10 km后的路程需加收50%的返空费(即单价为1.9×(1+50%)=2.85元/km).
(现实中要计等待时间且最终付费取整数,本题在计算时都不予考虑)
(1)将乘客搭乘一次B档出租车的费用f(x)(元)表示为行程x(0<x≤60,单位:km)的分段函数;
(2)某乘客行程为 16 km,他准备先乘一辆B档出租车行驶8 km,然后再换乘另一辆B档出租车完成余下行程,请问:他这样做是否比只乘一辆B档出租车完成全部行程更省钱?
16 km,他准备先乘一辆B档出租车行驶8 km,然后再换乘另一辆B档出租车完成余下行程,请问:他这样做是否比只乘一辆B档出租车完成全部行程更省钱?