我们在推导第一宇宙速度的公式v＝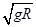
时，需要做一些假设和选择一些理论依据，下列必要的假设和理论依据有 ( )．
| A．卫星做半径等于2倍地球半径的匀速圆周运动 |
| B．卫星所受的重力全部作为其所需的向心力 |
| C．卫星所受的万有引力仅有一部分作为其所需的向心力 |
| D．卫星的运转周期必须等于地球的自转周期 |
关于万有引力定律应用于天文学研究的历史事实，下列说法中正确的是（）
| A．天王星、海王星和冥王星都是运用万有引力定律，经过大量计算以后而发现的 |
| B．在18世纪已发现的7个行星中，人们发现第七颗行星——天王星的运动轨道总是同根据万有引力定律计算出来的理论轨道有较大的偏差，于是有人推测，在天王星轨道之外还有一个行星，是它的存在引起了上述偏差 |
| C．海王星是牛顿运用了万有引力定律经过大量计算而发现的 |
| D．冥王星是英国剑桥大学的学生亚当斯和勒维列合作研究后共同发现的 |
利用下列哪组数据，可以计算出地球的质量（ ）
| A．地球的半径R地和地面的重力加速度g |
B．卫星绕地球做匀速圆周运动的半径R和周期T |
C．卫星绕地球做匀速圆周运动的半径R和线速度v |
D．卫星绕地球做匀速圆周运动的线速度v和周期T |
一飞船在某行星表面附近沿圆轨道绕该行星飞行，认为行星是密度均匀的球体，要确定该行星的密度，只需要测量（ ）
| A．飞船的轨道半径 |
| B．飞船的运行速度 |
| C．飞船的运行周期 |
| D．行星的质量 |
若已知行星绕太阳公转的半径为r，公转的周期为T，万有引力常量为G，则可求出（ ）
| A．某行星的质量 |
| B．太阳的质量 |
| C．某行星的密度 |
| D．太阳的密度 |
如图5-2-9所示,在河岸上用细绳拉船,为了使船匀速靠岸,拉绳的速度必须是( )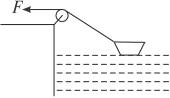
图5-2-9
| A．加速拉 | B．减速拉 | C．匀速拉 | D．先加速后减速 |