用数学归纳法证明“当n为正奇数时，xn＋yn能被x＋y整除”的第二步
是( )．
| A．假使n＝2k＋1时正确，再推n＝2k＋3正确 |
| B．假使n＝2k－1时正确，再推n＝2k＋1正确 |
| C．假使n＝k时正确，再推n＝k＋1正确 |
| D．假使n≤k(k≥1)，再推n＝k＋2时正确(以上k∈N＋) |
以下各数不能构成等差数列的是 ( )
| A．4,5,6 | B．1,4,7 |
C． ，， |
D．， ， |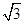
若sin α＋sin β＋sin γ＝0，cos α＋cos β＋cos γ＝0，则cos(α－β)＝( )．
| A．1 | B．－1 | C． |
D．－ |
p＝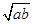
＋
，q＝
·
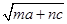(m、n、a、b、c、d均为正数)，
则p、q的大小为 ( )
| A．p≥q | B．p≤q | C．p＞q | D．不确定 |
设x，y∈R，且4xy＋4y2＋x＋6＝0，则x的取值范围是 ( )
| A．－3≤x≤2 | B．－2≤x≤3 |
| C．x≤－2或x≥3 | D．x≤－3或x≥2 |
的最大值为
，则函数
的图象的一条对称轴方程为
