设 是定义在
是定义在 上的可导函数,且满足
上的可导函数,且满足 . 若
. 若 且
且 ,则
,则
A. |
B. |
C. |
D. |
设 分别是双曲线
分别是双曲线 的两个焦点,P是该双曲线上的一点,且
的两个焦点,P是该双曲线上的一点,且 ,则
,则 的面积等于
的面积等于
A. |
B. |
C. |
D. |
用反证法证明命题“三角形的内角中至少有一个不大于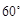 ”,则反设正确的是
”,则反设正确的是
A.假设三个内角中至少有一个大于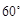 |
B.假设三个内角都不大于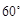 |
C.假设三个内角中至多有两个大于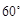 |
D.假设三个内角都大于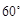 |
下列结论错误的是
A.“由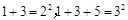 猜想 猜想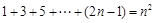 ”是归纳推理 ”是归纳推理 |
| B.合情推理的结论一定正确 |
| C.“由圆的性质类比出球的有关性质”是类比推理 |
| D.“三角形内角和是180°,四边形内角和是360°,五边形内角和是540°,由此得出凸多边形的内角和是(n-2)·180°”是归纳推理 |
若洗水壶要用1分钟、烧开水要用10分钟、洗茶杯要用2分钟、取茶叶要用1分钟、沏茶1分钟,那么较合理的安排至少也需要
| A.10分钟 | B.11分钟 |
C.12分钟 | D.13分钟 |