设函数f(x)(x∈R)满足f(-x)=f(x),f(x)=f(2-x),且当x∈[0,1]时,f(x)=x3.又函数g(x)=|xcos(πx)|,则函数h(x)=g(x)-f(x)在 上的零点个数为( )
上的零点个数为( )
| A.5 | B.6 | C.7 | D.8 |
正△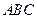 的边长为4,
的边长为4,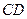 是
是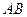 边上的高,
边上的高,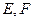 分别是
分别是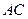 和
和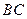 边的中点,现将△
边的中点,现将△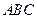 沿
沿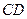 翻折成直二面角
翻折成直二面角 .
.
(1)试判断直线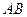 与平面
与平面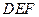 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)求二面角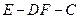 的余弦值;
的余弦值;
|
|
(3)在线段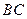 上是否存在一点
上是否存在一点 ,使
,使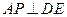 ?证明你的结论.
?证明你的结论.
 |
数列{an}是等差数列, ,
,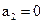 ,
,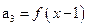 ,其中
,其中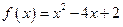 ,数列{an}前n项和存在最小值。
,数列{an}前n项和存在最小值。
(1)求通项公式an
(2)若 ,求数列
,求数列 的前n项和
的前n项和
如图,有一壁画,最高点A处离地面4m,最低点
B处离地面2m,若从离地高1.5m的 处观赏它,
处观赏它,
则离墙多远时,视角 最大?
最大?
在测量某物理量的过程中,因仪器和观察的误差,使得n次测量分别得到a1,a2,…an,共n个数据,我们规定所测量物理量的"最佳近似值"a是这样一个量:与其他近似值比较,a与各数据的差的平方和最小.依此规定,从a1,a2,…,an推出的a="" .
曲线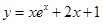 在点(0,1)处的切线方程为。
在点(0,1)处的切线方程为。