设命题p：非零向量a，b，|a|＝|b|是(a＋b)⊥(a－b)的充要条件；命题q：平面上M为一动点，A，B，C三点共线的充要条件是存在角α，使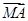
＝sin2α
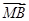＋cos2α
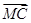，下列命题①p∧q；②p∨q；③¬p∧q；④¬p∨q.
其中假命题的序号是________．(将所有假命题的序号都填上)
如图，矩形ABCD中，AB=1，BC=a，PA⊥平面ABCD，若在BC上只有两个点Q满足PQ⊥DQ，则a的取值范围是 .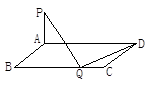
A,B是平面
外的两点，它们在平面内的射影分别是
,若A1A＝3,BB1="5," A1B1=10，那么线段AB的长是.
设m、n是平面α外的两条直线，给出三个论断：
①m∥n；②m∥α；③n∥α.以其中的两个为条件，余下的一个为结论，构造三个命题，写出你认为正确的一个命题：______________.(用序号表示)
以下命题（其中a，b表示直线，a表示平面）
①若a∥b，bÌa，则a∥a
②若a∥a，b∥a，则a∥b
③若a∥b，b∥a，则a∥a
④若a∥a，bÌa，则a∥b
其中正确命题的个数是 .
、△ABC所在平面α外一点P到三角形三顶点的距离相等，那么点P在α内的射影一定是△ABC的心（填“内”、”外”、“重”、“垂”）.