有三张正面分别写有数字﹣2，﹣1，1的卡片，它们的背面完全相同，将这三张卡片北背面朝上洗匀后随机抽取一张，以其正面的数字作为x的值，放回卡片洗匀，再从三张卡片中随机抽取一张，以其正面的数字作为y的值，两次结果记为（x，y）．
（1）用树状图或列表法表示（x，y）所有可能出现的结果；
（2）求使分式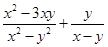
有意义的（x，y）出现的概率
（1）计算：
（2）解方程组：
已知抛物线y=-mx2+4x+2m与x轴交于点A（α，0）， B（β，0），且
．
（1）求抛物线的解析式．
（2）抛物线的对称轴为l，与y轴的交点为C，顶点为D，点C关于l的对称点为E．是否存在x轴上的点M、y轴上的点N，使四边形DNME的周长最小？若存在，请画出图形（保留作图痕迹），并求出周长的最小值；若不存在，请说明理由．
（3）若点P在抛物线上，点Q在x轴上，当以点D、E、P、Q为顶点的四边形是平行四边形时，求点P的坐标．
（1）问题
如图1，在四边形ABCD中，点P为AB上一点，∠DPC=∠A=∠B=90°．
求证：AD·BC=AP·BP．
（2）探究
如图2，在四边形ABCD中，点P为AB上一点，当∠DPC=∠A=∠B=θ时，上述结论是否依然成立？说明理由．
（3）应用
请利用（1）（2）获得的经验解决问题：
如图3，在△ABD中，AB=6，AD=BD=5．点P以每秒1个单位长度的速度，由点A出发，沿边AB向点B运动，且满足∠DPC=∠A．设点P的运动时间为t（秒），当以D为圆心，以DC为半径的圆与AB相切，求t的值．
某商店以40元/千克的单价新进一批茶叶，经调查发现，在一段时间内，销售量y（千克）与销售单价x（元/千克）之间的函数关系如图所示．
（1）根据图象，求y与x的函数关系式；
（2）商店想在销售成本不超过3000元的情况下，使销售利润达到2400元，销售单价应定为多少？
如图，⊙O的半径为1，A，P，B，C是⊙O上的四个点．∠APC=∠CPB=60°．
（1）判断△ABC的形状：；
（2）试探究线段PA，PB，PC之间的数量关系，并证明你的结论；
（3）当点P位于
的什么位置时，四边形APBC的面积最大？求出最大面积．