下列说法正确的是
A.“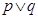 为真”是“ 为真”是“ 为真”的充分不必要条件; 为真”的充分不必要条件; |
B.设有一个回归直线方程为 ,则变量 ,则变量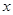 每增加一个单位, 每增加一个单位, 平均减少 平均减少 个单位; 个单位; |
C.若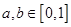 ,则不等式 ,则不等式 成立的概率是 成立的概率是 ; ; |
D.已知空间直线 ,若 ,若 , , ,则 ,则 . . |
已知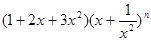 的展开式中没有常数项,
的展开式中没有常数项,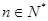 且
且 ,则
,则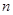 的值共( )
的值共( )
| A.1个 | B.2个 | C.4个 | D.0个 |
平面向量的集合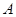 到
到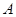 的映射
的映射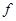 由
由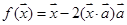 确定,其中
确定,其中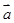 为常向量.若映射
为常向量.若映射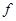 满足
满足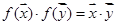 对
对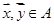 恒成立,则
恒成立,则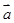 的坐标不可能是( )
的坐标不可能是( )
A.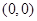 |
B.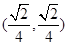 |
C.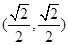 |
D.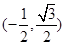 |
在下列结论中,正确的结论为()
(1)“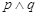 ”为真是“
”为真是“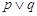 ”为真的充分不必要条件
”为真的充分不必要条件
(2)“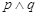 ”为假是“
”为假是“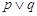 ”为真的充分不必要条件
”为真的充分不必要条件
(3)“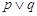 ”为真是“
”为真是“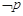 ”为假的必要不充分条件
”为假的必要不充分条件
(4)“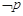 ”为真是“
”为真是“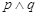 ”为假的必要不充分条件
”为假的必要不充分条件
| A.(1)(2) | B.(1)(3) |
| C.(2)(4) | D.(3)(4) |
如图,若程序框图输出的S是126,则判断框①中应为()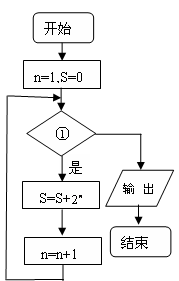
A.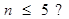 |
B.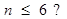 |
C.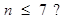 |
D.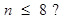 |
已知函数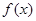 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当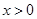 时,
时,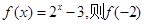 =
=
()
| A.1 | B.-1 | C. |
D. |