若圆心在x轴上、半径为
的圆C位于y轴左侧,且被直线x+2y=0截得的弦长为4,则圆C的方程是( )
| A．(x-)2+y2=5 |
B．(x+)2+y2=5 |
| C．(x-5)2+y2=5 | D．(x+5)2+y2=5 |
已知F1，F2是椭圆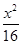
＋
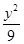＝1的两焦点，过点F2的直线交椭圆于A，B两点．在△AF1B中，若有两边之和是10，则第三边的长度为( )
| A．6 | B．5 | C．4 | D．3 |
“－3<m<5”是“方程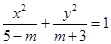
表示椭圆”的( )
| A．充分不必要条件 | B．必要不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |
下面四个条件中，使a＞b成立的充分而不必要的条件是( )
| A．a＞b＋1 | B．a＞b－1 | C．a2＞b2 | D．a3＞b3 |
命题“存在一个无理数，它的平方是有理数”的否定是( )
| A．任意一个有理数，它的平方是有理数 |
| B．任意一个无理数，它的平方不是有理数 |
| C．存在一个有理数，它的平方是有理数 |
| D．存在一个无理数，它的平方不是有理数 |
命题“若x，y都是偶数，则x＋y也是偶数”的逆否命题是( )
| A．若x＋y是偶数，则x与y不都是偶数 |
| B．若x＋y是偶数，则x与y都不是偶数 |
| C．若x＋y不是偶数，则x与y不都是偶数 |
| D．若x＋y不是偶数，则x与y都不是偶数 |