设A,B分别是直线y=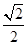 x和y=-
x和y=-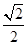 x上的动点,且|AB|=
x上的动点,且|AB|= ,设O为坐标原点,动点P满足
,设O为坐标原点,动点P满足 =
=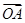 +
+ .
.
(1)求点P的轨迹方程;
(2)过点( ,0)作两条互相垂直的直线l1,l2,直线l1,l2与点P的轨迹的相交弦分别为CD,EF,设CD,EF的弦中点分别为M,N,求证:直线MN恒过一个定点.
,0)作两条互相垂直的直线l1,l2,直线l1,l2与点P的轨迹的相交弦分别为CD,EF,设CD,EF的弦中点分别为M,N,求证:直线MN恒过一个定点.
设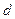 为非零实数,
为非零实数,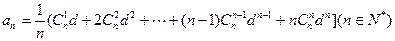
(Ⅰ)写出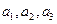 并判断
并判断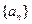 是否为等比数列.若是,给出证明;若不是,说明理由;
是否为等比数列.若是,给出证明;若不是,说明理由;
(Ⅱ)设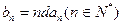 ,求数列
,求数列 的前n项和
的前n项和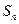 .
.
已知圆x2+y2+x-6y+m=0和直线x+2y-3=0交于P、Q两点.
(Ⅰ)求实数m的取值范围;
(Ⅱ)求以PQ为直径且过坐标原点的圆的方程.
一座抛物线拱桥在某时刻水面的宽度为52米,拱顶距离水面6.5米.
(Ⅰ)建立如图所示的平面直角坐标系xOy,试求拱桥所在抛物线的方程;
(Ⅱ)若一竹排上有一4米宽6米高的大木箱,问此木排能否安全通过此桥?
设函数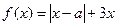 ,其中
,其中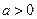 .
.
(Ⅰ)当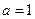 时,求不等式
时,求不等式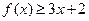 的解集;
的解集;
(Ⅱ)若不等式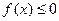 的解集为
的解集为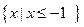 ,求a的值.
,求a的值.
(本小题满分10分)如图,在 △
△ 中,
中,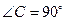 ,
, 平分
平分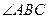 交
交 于点
于点 ,点
,点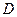 在
在 上,
上, .
.
(Ⅰ)求证: 是△
是△ 的外接圆的切线;
的外接圆的切线;
(Ⅱ)若 ,求
,求 的长.
的长.