已知曲线C的极坐标方程为ρ2=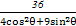
,以极点为原点,极轴所在直线为x轴建立平面直角坐标系.
(1)求曲线C的直角坐标方程及参数方程.
(2)若P(x,y)是曲线C上的一个动点,求x+2y的最小值,并求P点的坐标.
已知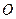
为坐标原点，
，
．
（Ⅰ）求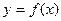
的单调递增区间；
（Ⅱ）若
的定义域为
，值域为[2，5]，求
的值。
已知数列{
}、{
}满足：
。
（Ⅰ）求
；
（Ⅱ）设
，求数列
的通项公式；
（Ⅲ）设
，不等式
恒成立时，求实数
的取值范围。
已知函数
，其定义域为
（
），设
。
（Ⅰ）试确定
的取值范围，使得函数
在上为单调函数；
（Ⅱ）试判断
的大小并说明理由；
（Ⅲ）求证：对于任意的,总存在
，满足
,并确定这样的
的个数。
设
为正实数，
，
，
。
（Ⅰ）如果
，则是否存在以
为三边长的三角形？请说明理由；
（Ⅱ）对任意的正实数
，试探索当存在以为三边长的三角形时
的取值范围。
已知
为坐标原点，
，
。
（Ⅰ）求
的单调递增区间；
（Ⅱ）若
的定义域为
，值域为
，求
的值。