某一运动物体,在x(s)时离出发点的距离(单位:m)是f(x)=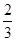 x3+x2+2x.
x3+x2+2x.
(1)求在第1s内的平均速度;
(2)求在1s末的瞬时速度;
(3)经过多少时间该物体的运动速度达到14m/s?
已知命题 方程
方程 的图象是焦点在
的图象是焦点在 轴上的双曲线;命题
轴上的双曲线;命题 方程
方程 无实根;又
无实根;又 为真,
为真, 为真,求实数
为真,求实数 的取值范围.
的取值范围.
设各项均为正数的数列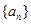 的前
的前 项和为
项和为 ,满足
,满足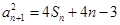 ,且
,且 恰好是等比数列
恰好是等比数列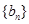 的前三项.
的前三项.
(1)求数列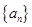 、
、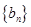 的通项公式;
的通项公式;
(2)记数列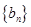 的前
的前 项和为
项和为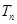 ,若对任意的
,若对任意的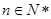 ,
,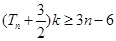 恒成立,求实数
恒成立,求实数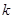 的取值范围.
的取值范围.
已知数列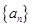 与
与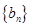 满足
满足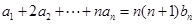 ,
,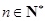 .
.
(1)若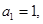
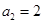 ,求
,求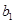 ,
, ;
;
(2)若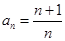 ,求证:
,求证: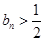 ;
;
(3)若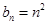 ,求数列
,求数列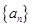 的通项公式.
的通项公式.
已知数列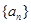 为等差数列,其中
为等差数列,其中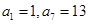 .
.
(1)求数列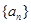 的通项公式;
的通项公式;
(2)若数列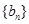 满足
满足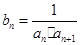 ,
, 为数列
为数列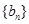 的前
的前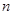 项和,当不等式
项和,当不等式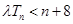 (
(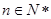 )恒成立时,求实数
)恒成立时,求实数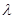 的取值范围.
的取值范围.
为了降低能源损耗,某体育馆的外墙需要建造隔热层.体育馆要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度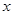 (单位:cm)满足关系:
(单位:cm)满足关系: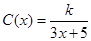 (
(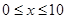 ,
,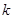 为常数),若不建隔热层,每年能源消耗费用为8万元.设
为常数),若不建隔热层,每年能源消耗费用为8万元.设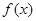 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(1)求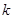 的值及
的值及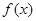 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用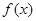 达到最小?并求最小值.
达到最小?并求最小值.