如图所示,边长为L的正方形区域abcd内存在着匀强电场电量为q、动能为Ek的带电粒子从a点沿ab方向进入电场,不计重力。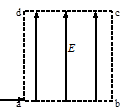
(1)若粒子从c点离开电场,求电场强度的大小和粒子离开电场时的动能;
(2)若粒子离开电场时动能为Ek’,则电场强度为多大?
如图所示,质量为m=4kg的物体静止在水平面上,在外力F=25N力的作用下 开始运动。已知F与水平方向夹角
开始运动。已知F与水平方向夹角 =37˚。当物体运动位移为5m时,物体具有5m/s的速度。求:(取g=10m/s2)
=37˚。当物体运动位移为5m时,物体具有5m/s的速度。求:(取g=10m/s2)
(1 ) 此过程中,物体克服摩擦力所做
) 此过程中,物体克服摩擦力所做 的功; (sin370="0.6" , cos370=0.8)
的功; (sin370="0.6" , cos370=0.8)
(2) 物体与水平面间的动摩擦因数。
宇航员到达某行星表面后,用长为 的细线拴一小球,让球在竖直面内做圆周运动。他测得当球通过最高点的速度为
的细线拴一小球,让球在竖直面内做圆周运动。他测得当球通过最高点的速度为 时,绳
时,绳 中张力刚好为零。设行星的半径为R、引力常量为G,求:
中张力刚好为零。设行星的半径为R、引力常量为G,求:
(1)该行星表面的重力加速度大小
(2)该行星的质量
(3)在该行星表面发射卫星所需要的最小速度
如图一辆质量为500kg的汽车静止在一座半径为50m的圆弧形拱桥顶部.(取g=10m/s2)
(1)此时汽车对 圆弧形拱桥的
圆弧形拱桥的 压力是多大?
压力是多大?
(2)如果汽车以6m/s的速度经过拱桥的顶部,则汽车对圆弧形拱桥的压力是多大
半径为R的半圆形光滑轨道竖直固定在水平地面上,A点是最低点,B 点是最高点,如图所示,质量为M的小球以某一速度自A点进入轨道,它经过最高点后飞出,最后落在水平地面上的C点,现测得AC=2R,求:
点是最高点,如图所示,质量为M的小球以某一速度自A点进入轨道,它经过最高点后飞出,最后落在水平地面上的C点,现测得AC=2R,求: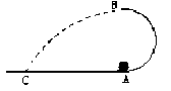
(1)小球从B点水平飞出时的速度是多少?
(2)小球自A点进入轨道时的速度大小?
(3)若轨道不光滑,小球从A点到B点需克服阻力做功 0.5mgR,则小球自A点进入轨道时的速度应该多大?
0.5mgR,则小球自A点进入轨道时的速度应该多大?
如图所示,一个质量为m=2㎏的物体,受到与水平方向成37°角斜向下方的推力F=10N作用,在水平地面上由静止开始移动了距离s=2m后撤去推力,此后物体又滑行了一段距离后停止了运动。设物体与地面间的动摩擦因数为0.2,求:
(1)推力F对物体做的功;
(2)撤去力F时,物体的速度;
(3)全过程中摩擦力对物体所做的功。