(13分)有一个小圆环瓷片最高能从h=0.18m高处静止释放后直接撞击地面而不被摔坏。现让该小圆环瓷片恰好套在一圆柱体上端且可沿圆柱体下滑,瓷片与圆柱体之间的摩擦力是瓷片重力的4.5倍,如图所示。若将该装置从距地面H=4.5m高处从静止开始下落,瓷片落地恰好没摔坏。已知圆柱体与瓷片所受的空气阻力都为自身重力的0.1倍,圆柱体碰地后速度立即变为零且保持竖直方向。(g=10m/s2)
⑴瓷片直接撞击地面而不被摔坏时,瓷片着地时的最大速度为多少?
⑵瓷片随圆柱体从静止到落地,下落总时间为多少?
如图所示,在倾角为37°的光滑斜面上有一根长为0.4 m,质量为6×10-2 kg的通电直导线,电流强度I=1 A,方向垂直于纸面向外,导线用平行于斜面的轻绳拴住不动,整个装置放在磁感应强度每秒增加0.4 T,方向竖直向上的磁场中.设t=0时,B=0,则需要多长时间斜面对导线的支持力为零?(g取10 m/s2)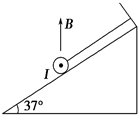
如图所示,M为一线圈电阻r=0.4Ω的电动机,R=24Ω,电源电动势E=40V.当S断开时,电流表的示数,I1=1.6A,当开关S闭合时,电流表的示数为I2=4.0A求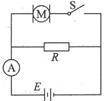
(1)电源内阻。
(2)开关S闭合时电动机发热消耗的功率和转化为机械能的功率。
(3)开关S闭合时电源的输出功率和电动机的机械效率。
如图所示,物体A.B各重10N ,水平拉力F1= 4N,F2=2N,物体保持静止,则A.B间的静摩擦力大小为多少?B与地面间的摩擦力大小为多少?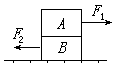
一物体做匀加速直线运动,在第1s内、第2s内通过的位移分别为1m和2m。问:加速度是多大?初速度又是多大?
如图所示,AB为竖直墙壁,A点和P点在同一水平面上。空间存在着竖直方向的匀强电场。将一带电小球从P点以速度v0向A抛出,结果打在墙上的C处。若撤去电场,将小球从P点以初速v0/2向A抛出,也正好打在墙上的C点。求:
(1)第一次抛出后小球所受电场力和重力之比
(2)小球两次到达C点时竖直速度之比