相距L=1.5m的足够长金属导轨竖直放置，质量为m1=1.0kg的金属棒ab和质量为m2=0.27kg的金属棒cd均通过棒两端的套环水平地套在金属导轨上，确保金属棒与金属导轨良好接触，如图（a）所示。虚线上方磁场方向垂直纸面向里，虚线下方磁场方向竖直向下，两处磁场磁感应强度大小相同。ab棒光滑，cd棒与导轨间动摩擦因数为μ=0.75，两棒总电阻为R=1.8Ω，导轨电阻不计。现有一方向竖直向下、大小按图（b）所示规律变化的外力F作用在ab棒上，使棒从静止开始沿导轨匀加速运动，与此同时cd棒也由静止释放。取重力加速度g=10m/s2。求：
（1）磁感应强度B的大小和ab棒的加速度大小；
（2）若在2s内外力F做功40J，则这一过程中两金属棒产生的总焦耳热是多少？
（3）判断cd棒将做怎样的运动，并求出cd棒达到最大速度所需的时间t0。
某市规定,卡车在市区行驶的速度不得超过40km/h。一次一辆飞驰的卡车在危急情况下刹车,经t=1.5s停止,民警量得这一过程中车轮在路面上擦过的痕迹长x=9m,据此能否判断这辆卡车是否超速违章?(设卡车从刹车开始至停下做匀减速直线运动)
一列全长为100米的火车，正在以2m/s2的加速度作匀加速度直线运动，它想要通过正前方一座全长是150米的大桥，当它的车头离桥头还有50米时，它的速度是5m/s，求该火车通过此桥的时间是多少？
一位汽车旅游爱好者打算到某风景区去观光，出发地和目的地之间是一条近似于直线的公路，他原计划全程平均速度要达到40 km/h，若这位旅游爱好者开出1/3路程之后发现他的平均速度仅有20 km/h，那么他能否完成全程平均速度为40 km/h的计划呢？若能完成，要求他在后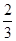
的路程里开车的速度应达多少？
一块质量为0.3kg的木块以速度v0在光滑水平面上运动,一个1.8N的力与运动方向相反作用木块上.从这个力作用在木块上时算起,木块移动9.0m的时候,木块的速度减到原来的一半,求这段运动所用的时间是多少?
如图12—2所示，布满了肥皂膜的金属框，AB是活动边，长5cm．如果重量和摩擦均不计，求肥皂膜作用到AB活动边上的表面张力．（肥皂液表面张力系数σ为20×10-3N／m）