如图甲所示,质量m=2 kg的物体在水平面上向右做直线运动。过a点时给物体作用一个水平向左的恒力F并开始计时,选水平向右为速度的正方向,通过速度传感器测出物体的瞬时速度,所得v-t图象如图乙所示。取重力加速度g=10 m/s2。求:
(1)力F的大小和物体与水平面间的动摩擦因数μ; (2)10s末物体离a点的距离。
质量为M="6" kg的木板B静止于光滑水平面上,物块A质量为6 kg,停在B的左端。质量为1 kg的小球用长为0. 8 m的轻绳悬挂在固定点O上,将轻绳拉直至水平位置后,由静止释放小球,小球在最低点与A发生碰撞后反弹,反弹所能达到的最大高度为0.2 m,物块与小球可视为质点,不计空气阻力。已知A、B间的动摩擦因数 ,为使A、B达到共同速度前A不滑离木板,木板至少多长?
,为使A、B达到共同速度前A不滑离木板,木板至少多长?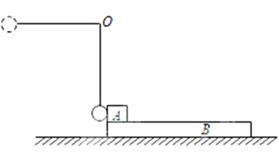
某种材料做成的一个底角为30°的等腰三棱镜,一细束红光从AB面的中点P沿平行于底面BC方向射入棱镜,经BC面反射,再从AC面的Q点射出,且有PQ∥BC(图中未画出光在棱镜内的光路),设真空中的光速为c,求: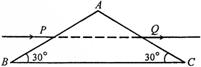
①该棱镜对红光的折射率;
②红光在棱镜中的传播速度。
如图所示,封闭有一定质量理想气体的汽缸固定在水平桌面上,开口向右放置,活塞的横截面积为S。活塞通过轻绳连接了一个质量为m的小物体,轻绳跨在定滑轮上。开始时汽缸内外压强相同,均为大气压
 。汽缸内气体的温度
。汽缸内气体的温度 ,轻绳处在伸直状态。不计摩擦。缓慢降低汽缸内温度,最终使得气体体积减半,求:
,轻绳处在伸直状态。不计摩擦。缓慢降低汽缸内温度,最终使得气体体积减半,求:
①重物刚离地时气缸内的温度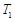 ;
;
②气体体积减半时的温度 ;
;
③在下列坐标系中画出气体状态变化的整个过程。并标注相关点的坐标值。
在如图甲所示的平面坐标系内,有三个不同的静电场:第一象限内有电荷量为Q的点电荷在O点产生的电场E1,第二象限内有水平向右的匀强电场E2(大小未知),第四象限内有方向水平、大小按图乙变化的电场E3,E3以水平向右为正方向,变化周期 。一质量为m,电荷量为+q的离子从(-x0,x0)点由静止释放,进入第一象限后恰能绕O点做圆周运动。以离子经过x轴时为计时起点,已知静电力常量为k,不计离子重力。求:
。一质量为m,电荷量为+q的离子从(-x0,x0)点由静止释放,进入第一象限后恰能绕O点做圆周运动。以离子经过x轴时为计时起点,已知静电力常量为k,不计离子重力。求:
(1)离子刚进入第四象限时的速度;
(2)E2的大小;
(3)当t= 时,离子的速度;
时,离子的速度;
(4)当t=nT时,离子的坐标。
如图所示,一固定的足够长的粗糙斜面与水平面夹角 .一个质量
.一个质量 的小物体(可视为质点),在F=10 N的沿斜面向上的拉力作用下,由静止开始沿斜面向上运动.已知斜面与物体间的动摩擦因数
的小物体(可视为质点),在F=10 N的沿斜面向上的拉力作用下,由静止开始沿斜面向上运动.已知斜面与物体间的动摩擦因数 ,取
,取 .试求:
.试求:
(1)物体在拉力F作用下运动的加速度 ;
;
(2)若力F作用1.2 s后撤去,物体在上滑过程中距出发点的最大距离s;