汤姆孙测定电子比荷（电子的电荷量与质量之比）的实验装置如图所示。真空玻璃管内，阴极K发出的电子经加速后，穿过小孔A、C沿中心轴线OP1进入到两块水平正对放置的极板D1、D2间的区域，射出后到达右端的荧光屏上形成光点。若极板D1、D2间无电压，电子将打在荧光屏上的中心P1点；若在极板间施加偏转电压U，则电子将打P2点，P2与P1点的竖直间距为b，水平间距可忽略不计。若再在极板间施加一个方向垂直于纸面向外、磁感应强度为B的匀强磁场（图中未画出），则电子在荧光屏上产生的光点又回到P1点。已知极板的长度为L1，极板间的距离为d，极板右端到荧光屏间的距离为L2。忽略电子的重力及电子间的相互作用。
（1）求电子进入极板D1、D2间区域时速度的大小；
（2）推导出电子的比荷的表达式；
（3）若去掉极板D1、D2间的电压，只保留匀强磁场B，电子通过极板间的磁场区域的轨迹为一个半径为r的圆弧，阴极射线射出极板后落在荧光屏上的P3点。不计P3与P1点的水平间距，求P3与P1点的竖直间距y。
在航天事业中要用角速度计可测得航天器自转的角速度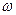
，其结构如图所示，当系统绕OO/转动时，元件A在光滑杆上发生滑动，并输出电信号成为航天器的制导信号源。已知A质量为m，弹簧的劲度系数为k，原长为L0，电源电动势为E，内阻不计，滑动变阻器总长为L，电阻分布均匀，系统静止时滑动变阻器触头P在中点，与固定接头Q正对，当系统以角速度
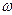转动时，求：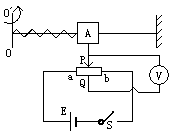
（1）弹簧形变量x与
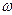的关系式；
（2）电压表的示数U与角速度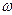的关系式
根据如图所示的振动图象：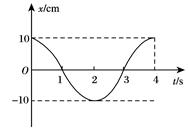
(1)算
出下列时刻振子对平衡位置的位移.
①t1="0.5" s;②t2=1.
5s.
(2)将位移时间的变化规律写成x=Asin(ωt+φ)的
形式并指出振动的初相位.
如图所示，在连有电阻R=3r的裸铜线框ABCD上，以AD为对称轴放置另一个正方形的小裸铜线框abcd，整个小线框处于垂直框面向里、磁感强度为B的匀强磁场中．已知
小线框每边长L，每边电阻为r,其它电阻不计。现使小线框以速度v向右平移，求通过电阻R的电流及R两端的电压．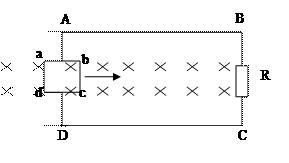
已知地球半径为R，地球表面重力加速度为g，不考虑地球自转的影响。
（1）推导第一宇宙速度v1的表达式；
（2）若卫星绕地球做匀速圆周运动，运行轨道距离地面高度为h，求卫星的运行
周期T。
如图，光滑水平面上有两枚铁钉A和B，它们相距0.2m,长1m的柔软细线拴在A上,另一端系一个质量为0.5kg的小球,小球的初始位置在AB连线上A的一侧,且细线伸直,给小球以3m/s垂直细线方向的水平速度使它做圆周运动,由于钉子B的存在,使线逐渐缠在AB上,求:
(1)如果细线不会断裂,从
小球开始运动到完全缠在AB上所需要的时间。
(2)如果细线的抗断力为9N,从开始运动到线断裂需多长时间?