（1）开普勒行星运动第三定律指出：行星绕太阳运动的椭圆轨道的半长轴a的三次方与它的公转周期T的二次方成正比，即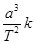
, 
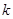是一个对所有行星都相同的常量。将行星绕太阳的运动按圆周运动处理，请你推导出太阳系中该常量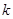的表达式。已知引力常量为G，太阳的质量为M太。
（2）开普勒定律不仅适用于太阳系，它对一切具有中心天体的引力系统（如地月系统）都成立。经测
定月地距离为3．84×108m，月球绕地球运动的周期为2．36×106s，试计算地球的质量M地。（G=6．67
×10-11N·m2/kg2，结果保留一位有效数字）
绳的一端固定，另一端系一质量为m=0.5kg的小球，绳长l=60cm，使小球在竖直平面内做圆周运动，重力加速度g=10m/s2，求：
（1）小球刚好能做圆周运动，在最高点的速度为多大？
（2）小球在最高点速率v=3m/s时，绳对小球的拉力为多大？
“神州六号”飞船的成功飞行为我国在2010年实现探月计划——“嫦娥工程”获得了宝贵的经验．假设月球半径为R，月球表面的重力加速度为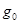
，飞船在距月球表面高度为3R的圆形轨道Ⅰ运动，到达轨道的A点点火变轨进入椭圆轨道Ⅱ，到达轨道的近月点B再次点火进入月球近月轨道Ⅲ绕月球作圆周运动．求：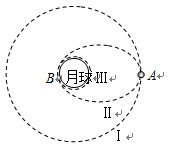
（1）飞船在轨道Ⅰ上的运行速率；
（2）飞船在轨道Ⅲ绕月球运行一周所需的时间．
小球自h=2m的高度由静止释放，与地面碰撞后反弹的高度为
h.设碰撞时没有动能的损失，且小球在运动过程中受到的空气阻力大小不变，且以后每碰撞地面一次弹起的高度为碰前的倍 .求：
（1）小球受到的空气阻力是重力的多少倍？
（2）小球运动的总路程.
一质量m="4.0" kg的物体，由高h="2.0" m，倾角θ=53°的固定斜面顶端滑到底端.物体与斜面间的动摩擦因数为μ=0.2.求物体所受各个力所做的功及所受合外力做的功.（g取10 m/s2)
一种氢气燃料的汽车，质量为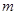
=2.0×103kg，发动机的额定输出功率为80kW，行驶在平直公路上时所受阻力恒为车重的0.1倍。若汽车从静止开始先匀加速启动，加速度的大小为
=1.0m/s2。达到额定输出功率后，汽车保持功率不变又加速行驶了800m，直到获得最大速度后才匀速行驶。试求：
（1）汽车的最大行驶速度；
（2）当汽车的速度为32m/s时的加速度；
（3）汽车从静止到获得最大行驶速度所用的总时间。