电磁感应现象是电磁学中最重大的发现之一，它揭示了电、磁现象之间的本质联系。
电路中感应电动势的大小，跟穿过这一电路的磁通量的变化率成正比，即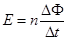
，这就是法拉第电磁感应定律。
（1）如图所示，把矩形线框abcd放在磁感应强度为B的匀强磁场里，线框平面跟磁感线垂直。设线框可动部分ab的长度为L，它以速度v向右匀速运动。请根据法拉第电磁感应定律推导出闭合电路的感应电动势E=BLv。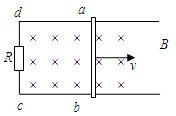
（2）两根足够长的光滑直金属导轨平行放置在倾角为θ的绝缘斜面上，两导轨间距为L。两导轨间接有阻值为R的电阻。一根质量为m的均匀直金属杆MN放在两导轨上，并与导轨垂直。整套装置处于磁感应强度为B匀强磁场中，磁场方向垂直于斜面向上。导轨和金属杆的电阻可忽略。让金属杆MN由静止沿导轨开始下滑。求
①当导体棒的速度为v（未达到最大速度）时，通过MN棒的电流大小和方向；
②导体棒运动的最大速度。
如图所示，AB是倾角为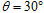
的粗糙直轨道，BCD是光滑的圆弧轨道，AB恰好在B点与圆弧相切，圆弧的半径为R，一个质量为m的物体（可以看做质点）从直轨道上的P点由静止释放，结果它能在两轨道间做往返运动。已知P点与圆弧的圆心O等高，物体与轨道AB间的动摩擦因数为μ。求：
（1）物体做往返运动的整个过程中在AB轨道上通过的总路程；
（2）最终当物体通过圆弧轨道最低点E时，对圆弧轨道的压力；
（3）为使物体能顺利到达圆弧轨道的最高点D，释放点距B点的距离L′至少多大。
如图所示，可视为质点的A、B两物体置于一静止长纸带上，纸带左端与A、A与B间距均为d =0.5m，两物体与纸带间的动摩擦因数均为
，与地面间的动摩擦因数均为
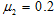。现以恒定的加速度a=2m/s2向右水平拉动纸带，重力加速度g= l0m/s2。求：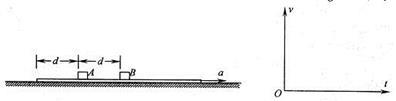
（1）A物体在纸带上的滑动时间；
（2）在给定的坐标系中定性画出A、B两物体的v-t图象；
（3）两物体A、B停在地面上的距离。
“嫦娥一号”卫星开始绕地球在椭圆轨道运动，经过变轨、制动后，成为一颗绕月球做圆周运动的卫星。设卫星距月球表面的高度为h ，做匀速圆周运动的周期为T 。已知月球半径为R ，引力常量为G。求：
（1）月球的质量M及月球表面的重力加速度g；
（2）在距月球表面高度为h0的地方（
），将一质量为m的小球以v0的初速度水平抛出，求落地瞬间月球引力对小球做功的瞬时功率P。
如图所示的电路中，两平行金属板A、B水平放置，两板间的距离d＝20 cm。电源电动势E＝24 V，内阻r＝1 Ω，电阻R＝15 Ω。闭合开关S，待电路稳定后，将一带正电的小球从B板小孔以初速度v0＝4 m／s竖直向上射入板间。若小球带电荷量为q＝1×10－2 C，质量为m＝2×10－2 kg，不考虑空气阻力。那么，滑动变阻器接入电路的阻值为多大时，小球恰能到达A板？此时，电源的输出功率是多大？（g取10 m／s2）
一电荷量为q（q＞0）、质量为m的带电粒子在匀强电场的作用下，在t＝0时由静止开始运动，场强随时间变化的规律如图所示。不计重力，求在t＝0到t＝T的时间间隔内：
（1）粒子位移的大小和方向；
（2）粒子沿初始电场反方向运动的时间。