有一个带正电的金属球壳(厚度不计),其截面图如图a所示,O为球心,球壳P处开有半径远小于球半径的小孔。以O点为坐标原点,过P点建立x坐标轴,A点是坐标轴上的一点,x轴上各点电势如图b所示。电子从O点以v0的初速度沿x轴方向射出,依次通过P、A两点。则下列关于电子的描述正确的是 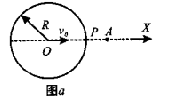

A在OP间电子做匀加速直线运动
B.在PA间电子做匀减速直线运动
C.在OP间运动时电子的电势能均匀增加
D.在PA间运动时电子的电势能增加
如图4所示,A、B两物块质量均为m,用一轻弹簧相连,将A用长度适当的轻绳悬挂于天花板上,系统处于静止状态,B物块恰好与水平桌面接触,此时轻弹簧的伸长量为x,重力加速度为g.现将悬绳剪断,则下列说法正确的是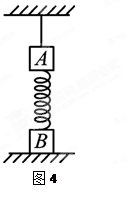
A.悬绳剪断瞬间,A物块的加速度大小为2g
B.悬绳剪断瞬间,A物块的加速度大小为g
C.悬绳剪断后,A物块向下运动距离x时速度最大
D.悬绳剪断后,A物块向下运动距离2x时速度最大
质量为2 kg的物体静止在足够大的水平地面上,物体与地面间的动摩擦因数为0.2,最大静摩擦力与滑动摩擦力大小视为相等.从t=0时刻开始,物体受到方向不变、大小呈周期性变化的水平拉力F的作用,F随时间t的变化规律如图3所示.重力加速度g取10 m/s2,则物体在t=0至t=12 s这段时间的位移大小为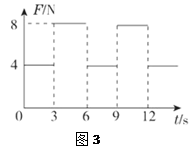
| A.18 m | B.54 m |
| C.72 m | D.198 m |
一辆公共汽车进站后开始刹车,做匀减速直线运动.开始刹车后的第1 s内和第2 s内位移大小依次为9 m和7 m,则刹车后6 s内的位移是
| A.20 m | B.24 m |
| C.25 m | D.75 m |
将质量为m的滑块放在倾角为θ的固定斜面上.滑块与斜面之间的动摩擦因数为μ。若滑块与斜面之间的最大静摩擦力和滑动摩擦力大小相等,重力加速度为g,则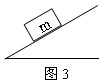
| A.将滑块由静止释放,如果μ>tanθ,滑块将下滑 |
| B.给滑块沿斜面向下的初速度,如果μ<tanθ,滑块将减速下滑 |
| C.用平行于斜面向上的力拉滑块向上匀速滑动,如果μ=tanθ,拉力大小应是2mgsinθ |
| D.用平行于斜面向下的力拉滑块向下匀速滑动,如果μ=tanθ,拉力大小是mgsinθ |
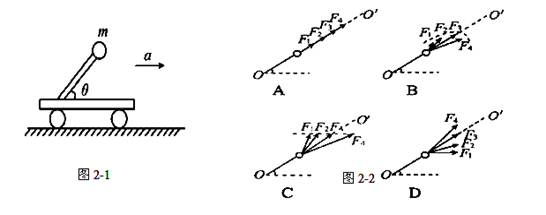
如图2-1所示,小车沿水平地面向右匀加速直线运动,固定在小车上的直杆与水平地面的夹角为θ,杆顶端固定有质量为m的小球.当小车的加速度逐渐增大时,杆对小球的作用力变化的受力图正确的是图2-2中的(OO′为沿杆方向)