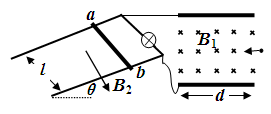
如图，两根足够长平行光滑的金属导轨相距为l，导轨与水平面夹角为θ,并处于磁感应强度为B2、方向垂直导轨平面向下的匀强磁场中。两金属导轨的上端与阻值为R的灯泡连接，并连接水平放置、长和宽都为d的平行金属板，板内存在垂直纸面向里的磁感应强度为B1的匀强磁场。长为l的金属棒ab垂直于金属导轨，且始终与导轨接触良好。当金属棒固定不动时，质量为m、电荷量为q的粒子流沿中线射入金属板内，恰好在金属板的左下边沿穿出。粒子重力不计，重力加速度为g，导轨和金属棒的电阻不计。
（1） 粒子流带何种电荷，速度多大？
（2） 现将金属棒由静止释放，待棒沿导轨匀速下滑后，粒子流水平通过，求金属棒质量M。
有两个完全相同的带电绝缘金属小球A、B，分别带有电荷量QA＝6.4×10－9C，QB＝－3.2×10－9C，让两绝缘金属小球接触，在接触过程中，电子如何转移并转移了多少？
现代理论认为，反质子的质量与质子相同，约为电子质量的1836倍．若me＝0.91×10－30kg，e＝1.6×10－19C，求反质子的比荷．
如图所示，电动机带动滚轮作逆时针匀速转动,在滚轮的摩擦力作用下,将一金属板从斜面底端A送往上部，已知斜面光滑且足够长，倾角θ=30°．滚轮与金属板的切点B到斜面底端A的距离为L=6.5m，当金属板的下端运动到切点B处时，立即提起滚轮使它与板脱离接触．已知板之后返回斜面底部与挡板相撞后立即静止，此时放下滚轮再次压紧板，再次将板从最底端送往斜面上部，如此往复．已知板的质量为m=1×103Kg，滚轮边缘线速度恒为v=4m/s，滚轮对板的正压力FN=2×104N，滚轮与板间的动摩擦因数为μ=0.35，取g=10m/s2．
求：(1)在滚轮作用下板上升的加速度；
(2)板加速至与滚轮速度相同时前进的距离；
(3)每个周期中滚轮对金属板所做的功；
(4)板往复运动的周期．
如图6所示，质量为m的小球，用不可伸长的线悬于固定点O，线长为l，初始线与铅垂线有一个夹角，初速为0. 在小球开始运动后，线碰到铁钉O1. 铁钉的方向与小球运动的平面垂直. OO1=h<l，且已知OO1与铅垂线夹角为β. 假设碰后小球恰能做圆周运动. 求线与铁钉碰前瞬时与碰后瞬时张力的变化.
用同种材料制成倾角30°的斜面和长水平面，斜面长2.4m且固定，一小物块从斜面顶端以沿斜面向下的初速度v0开始自由下滑，当v0="2" m/s时，经过0.8s后小物块停在斜面上多次改变v0的大小，记录下小物块从开始运动到最终停下的时间t，作出t-v0图象，如图所示，求：
1）小物块与该种材料间的动摩擦因数为多少？
2）某同学认为，若小物块初速度为4m/s，则根据图象中t与v0成正比推导，可知小物块运动时间为1.6s。以上说法是否正确？若不正确，说明理由并解出你认为正确的结果。