已知直线l1:4x-3y+6=0和直线l2:x=-1,抛物线y2=4x上一动点P,P到直线l1和直线l2的距离之和的最小值是( )
| A.2 | B.3 | C.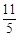 |
D.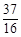 |
已知函数 则( )
则( )
| A.无法确定 | B. |
C. |
D. |
下列判断正确的是()
A.若命题 为真命题,命题 为真命题,命题 为假命题,则命题“ 为假命题,则命题“ ”为真命题 ”为真命题 |
B.命题“若 ,则 ,则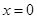 ”的否命题为“若 ”的否命题为“若 ,则 ,则 ” ” |
C.“ ”是“ ”是“  ”的充分不必要条件 ”的充分不必要条件 |
D.命题“ ”的否定是“ ”的否定是“ 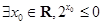 ” ” |
数列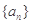 的前n项和
的前n项和 ,则通项公式
,则通项公式 为( )
为( )
A. |
B. |
C. |
D. |
下列结论中正确的是( )
| A.平行于平面内两条直线的平面,一定平行于这个平面 |
| B.一条直线平行于一个平面内的无数条直线,则这条直线与该平面平行 |
| C.两个平面分别与第三个平面相交,若交线平行则两平面平行 |
| D.在两个平行平面中,一平面内的一条直线必平行于另一个平面 |
若平面向量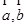 满足
满足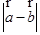 =
=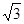 ,
,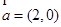 ,
,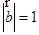 ,则平面向量
,则平面向量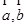 的夹角为( )
的夹角为( )
A.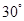 |
B.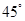 |
C.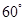 |
D.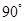 |