如图,四棱锥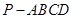 的底面
的底面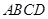 为一直角梯形,其中
为一直角梯形,其中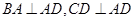 ,
,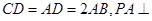 底面
底面 ,
,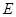 是
是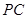 的中点.
的中点.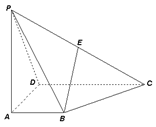
(Ⅰ)求证: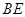 //平面
//平面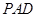 ;
;
(Ⅱ)若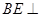 平面
平面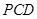 ,求平面
,求平面 与平面
与平面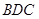 夹角的余弦值.
夹角的余弦值.
已知函数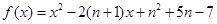 .
.
(Ⅰ)设函数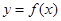 的图像的顶点的纵坐标构成数列
的图像的顶点的纵坐标构成数列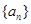 ,求证:
,求证: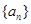 为等差数列;
为等差数列;
(Ⅱ)设函数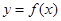 的图像的顶点到
的图像的顶点到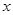 轴的距离构成数列
轴的距离构成数列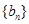 ,求
,求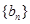 的前
的前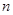 项和
项和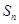 .
.
已知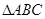 的三个内角
的三个内角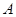 、
、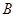 、
、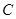 的对边分别为
的对边分别为 、
、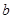 、
、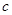 ,且
,且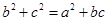 .
.
(Ⅰ) 求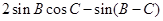 的值;
的值;
(Ⅱ)若 ,求
,求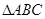 周长的最大值.
周长的最大值.
已知函数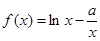 ,
, ,其中
,其中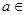 R .
R .
(1)讨论 的单调性;
的单调性;
(2)若 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数 的取值范围;
的取值范围;
(3)设函数 , 当
, 当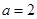 时,若存在
时,若存在 ,对于任意的
,对于任意的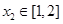 ,总有
,总有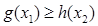 成立,求实数
成立,求实数 的取值范围.
的取值范围.
已知函数 (a,b为常数)且方程f(x)-x+12=0有两个实根为x1="3," x2=4.
(a,b为常数)且方程f(x)-x+12=0有两个实根为x1="3," x2=4.
(1)求函数f(x)的解析式;
(2)设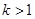 ,解关于x的不等式;
,解关于x的不等式; .
.