给出以下问题：
①求面积为1的正三角形的周长；
②求键盘所输入的三个数的算术平均数；
③求键盘所输入的两个数的最小数；
④求函数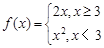
当自变量取
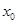时的函数值.
其中不需要用条件语句来描述算法的问题有( )
| A．1个 | B．2个 | C．3个 | D．4个 |
直线l经过l1: x＋y－2＝0与l2: x－y－4＝0的交点P，且过线段AB的
中点Q，其中A(－1,3), B(5,1)，则直线l的方程是（）
| A．3x－y－8＝0 | B．3x＋y＋8＝0 |
| C．3x＋y－8＝0 | D．3x－y＋8＝0 |
已知m, n是两条不同的直线，a, b是两个不同的平面，下列命题正确的是（）
| A．若m∥a, n∥a，则m∥n | B．若a⊥b, m⊥b, mËa, 则m∥a |
| C．若a⊥b, m//a, 则m⊥b | D．若mÌa, nÌa, m∥b, n∥b, 则a∥b |
一只蜜蜂在一个棱长为3的正方体内自由飞行，若蜜蜂在飞行过程中始终与正方体6个面的距离大于1称其为“安全飞行”，则蜜蜂安全飞行的概率为：（）
A． |
B． |
C． |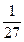
D． |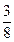
有3个兴趣小组，甲乙两位同学各自参加其中一个小组，每位同学参加各个小组的可能性相同，则这两位同学参加同一兴趣小组的概率为：（）
A． |
B． |
C． |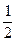
D． |
已知一组正数x1,x2,x3,x4的方差S2=
（x12+x22+x32+x42-16），则数据x1+2,x2+2,x3+2,x4+2的平均数为：（）
| A．2 | B．3 | C．4 | D．6 |