某校数学课题学习小组在“测量教学楼高度”的活动中,设计了以下两种方案:
| 课题 |
测量教学楼高度 |
|
| 方案 |
一 |
二 |
| 图示 |
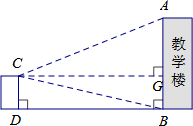 |
 |
| 测得数据 |
CD=6.9m,∠ACG=22°,∠BCG=13°, |
EF=10m,∠AEB=32°,∠AFB=43° |
| 参考数据 |
sin22°≈0.37,cos22°≈0.93, tan22°≈0.40 sin13°≈0.22,cos13°≈0.97 tan13°≈0.23 |
sin32°≈0.53,cos32°≈0.85,tan32°≈0.62 sin43°≈0.68,cos43°≈0.73,tan43°≈0.93 |
请你选择其中的一种方法,求教学楼的高度(结果保留整数)